题目内容
有一张矩形纸片ABCD,其中AD=4cm,以AD为直径的半圆,正好与对边BC相切,如图(甲),将它沿DE折叠,使A点落在BC上,如图(乙),这时,半圆还露在外面的部分(阴影部分)的面积是
分析:设半圆的圆心是O,半圆与AD交点是F,连接OF,作FG⊥A′D于G.根据AD=4,CD=2,得∠CAD=30°,则∠ODF=30°,则∠FOD=120°,从而求得扇形的面积;在直角三角形OFG中,根据锐角三角函数求得FG的长,从而求得三角形ODF的面积,进一步求得阴影部分的面积.
解答: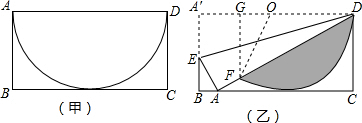 解:设半圆的圆心是O,半圆与AD交点是F,连接OF,作FG⊥A′D于G.
解:设半圆的圆心是O,半圆与AD交点是F,连接OF,作FG⊥A′D于G.
在Rt△ACD中,∵AD=4,CD⊥BC,
∴CD=
AD=2,
∴∠CAD=30°,
∴∠ODF=30°,
∴∠FOD=120°.
∴扇形ODF的面积=
=
π.
在Rt△OFG中,OF=2,∠FOG=60°,
∴FG=
.
∴△OFD的面积=
.
∴阴影部分的面积=
π-
.
故答案为:
π-
.
 解:设半圆的圆心是O,半圆与AD交点是F,连接OF,作FG⊥A′D于G.
解:设半圆的圆心是O,半圆与AD交点是F,连接OF,作FG⊥A′D于G.在Rt△ACD中,∵AD=4,CD⊥BC,
∴CD=
| 1 |
| 2 |
∴∠CAD=30°,
∴∠ODF=30°,
∴∠FOD=120°.
∴扇形ODF的面积=
| 120π×4 |
| 360 |
| 4 |
| 3 |
在Rt△OFG中,OF=2,∠FOG=60°,
∴FG=
| 3 |
∴△OFD的面积=
| 3 |
∴阴影部分的面积=
| 4 |
| 3 |
| 3 |
故答案为:
| 4 |
| 3 |
| 3 |
点评:此题关键是能够把不规则图形的面积转换为规则图形的面积,此题综合运用了折叠的图形全等的性质、切线的性质、扇形面积公式以及30°的直角三角形的性质.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
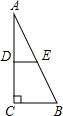 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( ) 如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一
如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一




 = ;
= ; 




 = ;
= ; 