题目内容
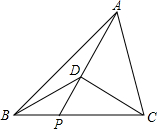 如图,点P为△ABC的BC边上一点,且PC=2PB,∠ABC=45°,∠APC=60°,CD⊥AP,连接BD,求∠ABD的度数.
如图,点P为△ABC的BC边上一点,且PC=2PB,∠ABC=45°,∠APC=60°,CD⊥AP,连接BD,求∠ABD的度数.
解:∵∠APC=60°,CD⊥AP,
∴∠PCD=90°-∠APC=90°-60°=30°,
∴PC=2PD,
∵PC=2PB,
∴PB=PD,
∴∠PBD=∠PDB,
又∵∠APC=∠PBD+∠PDB,
∴∠PBD= ∠APC=
∠APC= ×60°=30°,
×60°=30°,
∵∠ABC=45°,
∴∠ABD=∠ABC-∠PBD=45°-30°=15°.
分析:根据直角三角形两锐角互余求出∠PCD=30°,再根据直角三角形30°角所对的直角边等于斜边的一半可得PC=2PD,然后求出PB=PD,根据等边对等角可得∠PBD=∠PDB,再根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠PBD,然后求解即可.
点评:本题考查了直角三角形30°角所对的直角边等于斜边的一半,三角形的一个外角等于与它不相邻的两个内角的和的性质,直角三角形两锐角互余的性质,等边对等角的性质,熟记性质并准确识图是解题的关键.
∴∠PCD=90°-∠APC=90°-60°=30°,
∴PC=2PD,
∵PC=2PB,
∴PB=PD,
∴∠PBD=∠PDB,
又∵∠APC=∠PBD+∠PDB,
∴∠PBD=
 ∠APC=
∠APC= ×60°=30°,
×60°=30°,∵∠ABC=45°,
∴∠ABD=∠ABC-∠PBD=45°-30°=15°.
分析:根据直角三角形两锐角互余求出∠PCD=30°,再根据直角三角形30°角所对的直角边等于斜边的一半可得PC=2PD,然后求出PB=PD,根据等边对等角可得∠PBD=∠PDB,再根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠PBD,然后求解即可.
点评:本题考查了直角三角形30°角所对的直角边等于斜边的一半,三角形的一个外角等于与它不相邻的两个内角的和的性质,直角三角形两锐角互余的性质,等边对等角的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 12、如图,点H为△ABC的垂心,以AB为直径的⊙O1和△BCH的外接圆⊙O2相交于点D,延长AD交CH于点P,
12、如图,点H为△ABC的垂心,以AB为直径的⊙O1和△BCH的外接圆⊙O2相交于点D,延长AD交CH于点P, 25、尺规作图(不写作法,但要保留作图痕迹)
25、尺规作图(不写作法,但要保留作图痕迹)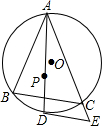 如图,点P为△ABC的内心,延长AP交△ABC的外接圆⊙O于D,过D作DE∥BC,交AC的延长线于E点.①则直线DE与⊙O的位置关系是
如图,点P为△ABC的内心,延长AP交△ABC的外接圆⊙O于D,过D作DE∥BC,交AC的延长线于E点.①则直线DE与⊙O的位置关系是 如图,点G为△ABC的重心,DE过点G,且DE∥BC,EF∥AB,那么CF:BF=
如图,点G为△ABC的重心,DE过点G,且DE∥BC,EF∥AB,那么CF:BF= 如图,点E为△ABC边AB上一点,AC=BC=BE,AE=EC,BD⊥AC于D,求∠CBD的度数.
如图,点E为△ABC边AB上一点,AC=BC=BE,AE=EC,BD⊥AC于D,求∠CBD的度数.