题目内容
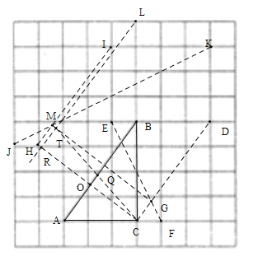
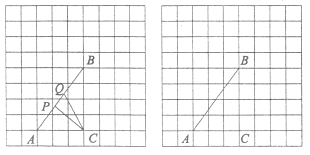
【题目】如图,在由边长都为1的小正方形组成的网格中,点![]() 均为格点,点
均为格点,点![]() 为线段
为线段![]() 上的动点,且满足
上的动点,且满足![]() .
.
(Ⅰ)当点Q为线段![]() 中点时
中点时![]() 的长度等于________.
的长度等于________.
(Ⅱ)当线段![]() 取得最小值时,请借助无刻度直尺在给定的网格中画出点Q,并简要说明你是怎么画出点Q的:_______.
取得最小值时,请借助无刻度直尺在给定的网格中画出点Q,并简要说明你是怎么画出点Q的:_______.
【答案】(Ⅰ)![]() (Ⅱ)取格点
(Ⅱ)取格点![]() ,连接
,连接![]() ,它们相交于点G,取格点
,它们相交于点G,取格点![]() .连接
.连接![]() ,它们相交于点M,连接
,它们相交于点M,连接![]() ,取格点
,取格点![]() .连接
.连接![]() 并延长,交
并延长,交![]() 于点T,连接
于点T,连接![]() ,交
,交![]() 于点Q,则点Q即为所求,见解析.
于点Q,则点Q即为所求,见解析.
【解析】
(Ⅰ)先根据勾股定理得出AB的长,再根据直角三角形斜边上的中线等于斜边的一半,即可求出![]() 的长度
的长度
(Ⅱ)取格点![]() ,连接
,连接![]() ,它们相交于点G,取格点
,它们相交于点G,取格点![]() .连接
.连接![]() ,它们相交于点M,连接
,它们相交于点M,连接![]() ,取格点
,取格点![]() .连接
.连接![]() 并延长,交
并延长,交![]() 于点T,连接
于点T,连接![]() ,交
,交![]() 于点Q,
于点Q,
解:(Ⅰ)在Rt![]() ,
,![]() ,
,
∴AB=![]() =5
=5
∵点Q为线段![]() 中点
中点
∴![]() ;
;
故答案为:![]()
(Ⅱ)线段![]() 取得最小值时,点P,Q必在线段AB的高线的垂足的两侧,并关于垂足对称,即离垂足的距离为0.5.所以先找到点C关于AB的对称点,首先先找垂线,因为AB是3×4的格点矩形的对角线,所以只需过点C作3×4的格点矩形的对角线CH即可满足CH⊥AB垂足为O,下一步找距离相等.可找到D点,构成3×4的格点矩形的对角线CD,则有CD∥AB,且BD=3,同样找到格点N,L使其为3×4的格点矩形的对角线端点,且BN=3,则有LN与CD到AB的距离相等且平行,延长LN则与CH相交R,则交点即为C关于AB的对称点.现要保证OQ=0.5,则只需在LR上找到点T,CD上找到点G,使得RT=CG=1,则四边形RCGT为矩形.因为CD=5,则只需找到CD的五等分点,找到格点E,F,使CF=1,DE=4,且CF∥ED,则CD与EF的交点为G.因为在LR上找的点T不能直接找到,我们可以过点H作AB的平行线HI,并在HI上找到点M使得HM=1,则MG与LR 的交点即为T点,且OT=1.则易找到格点I使得HI∥AB,同E,F的找法,找到格点J,K,连接JK交HI 于点M ,则HM=1,连接MG交LR于点T,再连接TC与AB的交点为Q,则点Q即为所求.
取得最小值时,点P,Q必在线段AB的高线的垂足的两侧,并关于垂足对称,即离垂足的距离为0.5.所以先找到点C关于AB的对称点,首先先找垂线,因为AB是3×4的格点矩形的对角线,所以只需过点C作3×4的格点矩形的对角线CH即可满足CH⊥AB垂足为O,下一步找距离相等.可找到D点,构成3×4的格点矩形的对角线CD,则有CD∥AB,且BD=3,同样找到格点N,L使其为3×4的格点矩形的对角线端点,且BN=3,则有LN与CD到AB的距离相等且平行,延长LN则与CH相交R,则交点即为C关于AB的对称点.现要保证OQ=0.5,则只需在LR上找到点T,CD上找到点G,使得RT=CG=1,则四边形RCGT为矩形.因为CD=5,则只需找到CD的五等分点,找到格点E,F,使CF=1,DE=4,且CF∥ED,则CD与EF的交点为G.因为在LR上找的点T不能直接找到,我们可以过点H作AB的平行线HI,并在HI上找到点M使得HM=1,则MG与LR 的交点即为T点,且OT=1.则易找到格点I使得HI∥AB,同E,F的找法,找到格点J,K,连接JK交HI 于点M ,则HM=1,连接MG交LR于点T,再连接TC与AB的交点为Q,则点Q即为所求.