题目内容
【题目】如图,在平面直角坐标系中,一次函数y=ax﹣a(a为常数)的图象与y轴相交于点A,与函数y=![]() 的图象相交于点B(m,1).
的图象相交于点B(m,1).
(1)求点B的坐标及一次函数的解析式;
(2)若点P在y轴上,且△PAB为直角三角形,请直接写出点P的坐标.
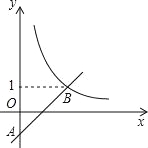
【答案】(1) B(2,1);y=x﹣1;(2) P(0,1)或(0,3).
【解析】
试题分析:(1)由点在函数图象上,得到点的坐标满足函数解析式,利用待定系数法即可求得;
(2)分两种情况,一种是∠BPA=90°,另一种是∠PBA=90°,所以有两种答案.
试题解析:(1)∵B在的图象上,
∴把B(m,1)代入y=![]() ,得m=2,
,得m=2,
∴B点的坐标为(2,1),
∵B(2,1)在直线y=ax﹣a(a为常数)上,
∴1=2a﹣a,
∴a=1,
∴一次函数的解析式为y=x﹣1;
(2)过B点向y轴作垂线交y轴于P点.此时∠BPA=90°,
∵B点的坐标为(2,1),
∴P点的坐标为(0,1),
当PB⊥AB时,在Rt△P1AB中,PB=2,PA=2,
∴AB=![]() ,
,
在等腰直角三角形PAB中,PB=PA=![]() ,
,
∴PA=![]() =4,
=4,
∴OP=4﹣1=3,
∴P点的坐标为(0,3),
∴P点的坐标为(0,1)或(0,3).


练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目