题目内容
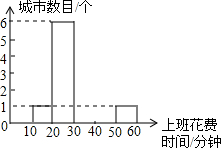
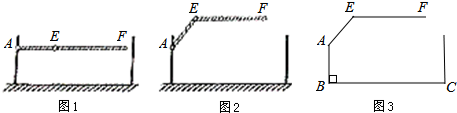
(2013•上海)某地下车库出口处“两段式栏杆”如图1所示,点A是栏杆转动的支点,点E是栏杆两段的连接点.当车辆经过时,栏杆AEF升起后的位置如图2所示,其示意图如图3所示,其中AB⊥BC,EF∥BC,∠EAB=143°,AB=AE=1.2米,求当车辆经过时,栏杆EF段距离地面的高度(即直线EF上任意一点到直线BC的距离).
(结果精确到0.1米,栏杆宽度忽略不计参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75.)
(结果精确到0.1米,栏杆宽度忽略不计参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75.)

分析:过点A作BC的平行线AG,过点E作EH⊥AG于H,则∠BAG=90°,∠EHA=90°.先求出∠EAH=53°,则∠EAH=53°,然后在△EAH中,利用余弦函数的定义得出EH=AE•cos∠AEH≈0.96米,则栏杆EF段距离地面的高度为:AB+EH,代入数值计算即可.
解答: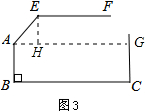 解:如图,过点A作BC的平行线AG,过点E作EH⊥AG于H,则∠BAG=90°,∠EHA=90°.
解:如图,过点A作BC的平行线AG,过点E作EH⊥AG于H,则∠BAG=90°,∠EHA=90°.
∵∠EAB=143°,∠BAG=90°,
∴∠EAH=∠EAB-∠BAG=53°.
在△EAH中,∠EHA=90°,∠AEH=90°-∠EAH=37°,AE=1.2米,
∴EH=AE•cos∠AEH≈1.2×0.80=0.96(米),
∵AB=1.2米,
∴栏杆EF段距离地面的高度为:AB+EH≈1.2+0.96=2.16≈2.2(米).
故栏杆EF段距离地面的高度约为2.2米.
 解:如图,过点A作BC的平行线AG,过点E作EH⊥AG于H,则∠BAG=90°,∠EHA=90°.
解:如图,过点A作BC的平行线AG,过点E作EH⊥AG于H,则∠BAG=90°,∠EHA=90°.∵∠EAB=143°,∠BAG=90°,
∴∠EAH=∠EAB-∠BAG=53°.
在△EAH中,∠EHA=90°,∠AEH=90°-∠EAH=37°,AE=1.2米,
∴EH=AE•cos∠AEH≈1.2×0.80=0.96(米),
∵AB=1.2米,
∴栏杆EF段距离地面的高度为:AB+EH≈1.2+0.96=2.16≈2.2(米).
故栏杆EF段距离地面的高度约为2.2米.
点评:本题考查了解直角三角形在实际中的应用,难度适中.关键是通过作辅助线,构造直角三角形,把实际问题转化为数学问题加以计算.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
2013年3月,上海、安徽两地率先发现H7N9型禽流感,某药店以每件50元价格购进800件治疗H7N9的某特效药,第一个月以单价80元销售,售出了200件;每第二个月如果单价不变,预计仍可售出200件药,药店为增加销量,决定降价销售,据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格,第二个月结束后,药店对剩余的H7N9特效药一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.
(1)填表(用含x的式子表示)
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | ______ | 40 |
| 销量(件) | 200 | ______ | ______ |
(2)若药店希望通过卖这批H7N9特效药获利9000元,则第二个月的单价应是多少?
2013年3月,上海、安徽两地率先发现H7N9型禽流感,某药店以每件50元价格购进800件治疗H7N9的某特效药,![]() 第一个月以单价80元销售,售出了200件;每第二个月如果单价不变,预计仍可售出200件药,药店为增加销量,决定降价销售,据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格,第二个月结束后,药店对剩余的H7N9特效药一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.
第一个月以单价80元销售,售出了200件;每第二个月如果单价不变,预计仍可售出200件药,药店为增加销量,决定降价销售,据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格,第二个月结束后,药店对剩余的H7N9特效药一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.
(1)填表(用含x的式子表示)
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | 40 | |
| 销量(件) | 200 |
(2)若药店希望通过卖这批H7N9特效药获利9000元,则第二个月的单价应是多少?
 (2013•铜仁地区)某中学组织部分优秀学生分别去北京、上海、天津、重庆四个城市进行夏令营活动,学校购买了前往四个城市的车票,如图是未制作完整的车票种类和数量的条形统计图,请你根据统计图回答下列问题:
(2013•铜仁地区)某中学组织部分优秀学生分别去北京、上海、天津、重庆四个城市进行夏令营活动,学校购买了前往四个城市的车票,如图是未制作完整的车票种类和数量的条形统计图,请你根据统计图回答下列问题: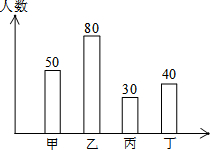 (2013•上海)某校报名参加甲、乙、丙、丁四个兴趣小组的学生人数如图所示,那么报名参加甲组和丙组的人数之和占所有报名人数的百分比为
(2013•上海)某校报名参加甲、乙、丙、丁四个兴趣小组的学生人数如图所示,那么报名参加甲组和丙组的人数之和占所有报名人数的百分比为