Question

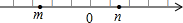实数m、n在数轴上的位置如图所示，那么化简|m-n|-

n2

的结果是（　　）

A．-m

B．m

C．2n-m

D．m-2n

Answer 1

分析：先根据数轴可知m＜0，n＞0，那么m-n就是负数，再根据绝对值的概念可知负数的绝对值等于它的相反数，可化简
|m-n|，再根据二次根式的性质可化简

n2

，最后合并同类项即可．

解答：解：根据数轴可知，
m＜0，n＞0，
∴原式=-（m-n）-n=-m+n-n=-m．
故选A．

点评：本题考查了二次根式的化简和性质，解题的关键是能根据数轴得出m、n的取值．