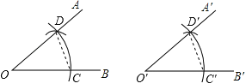题目内容
【题目】如图,在RtABC 中,ACB 90 , AC 3 ,BC 4 ,点 D在 AB上, AD AC , AF CD 交CD 于点 E ,交CB 于点 F ,则CF 的长是( )
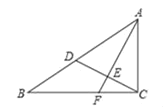
A. 2.5B. 2C. 1.8D. 1.5
【答案】D
【解析】
连接DF,由勾股定理求出AB=5,由等腰三角形的性质得出CE=DE,由线段垂直平分线的性质得出CF=DF,由SSS证明△ADF≌△ACF,得出∠ADF=∠ACF=∠BDF=90°,设CF=x,则DF=x,BF=4﹣x.在Rt△BDF中,由勾股定理得出方程,解方程即可.
连接DF,如图所示.
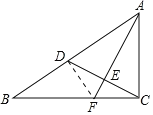
∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,∴AB![]() 5.
5.
∵AD=AC=3,AF⊥CD,∴CE=DE,BD=AB﹣AD=2,∴CF=DF.
在△ADF和△ACF中,∵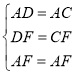 ,∴△ADF≌△ACF(SSS),∴∠ADF=∠ACF=90°,∴∠BDF=90°.设CF=x,则DF=x,BF=4﹣x.
,∴△ADF≌△ACF(SSS),∴∠ADF=∠ACF=90°,∴∠BDF=90°.设CF=x,则DF=x,BF=4﹣x.
在Rt△BDF中,由勾股定理得:DF2+BD2=BF2,即x2+22=(4﹣x)2,解得:x=1.5;∴CF=1.5.
故选D.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目