题目内容
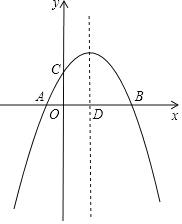
【题目】如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)经过点A(1,0)和点B(0,﹣2),且顶点在第三象限,记m=a﹣b+c,则m的取值范围是( )
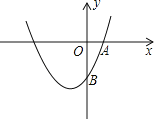
A. ﹣1<m<0B. ﹣2<m<0C. ﹣4<m<﹣2D. ﹣4<m<0
【答案】D
【解析】
求出a>0,b>0,把x=1代入求出a=2﹣b,b=2﹣a,把x=﹣1代入得出y=a﹣b+c=2a﹣4,求出2a﹣4的范围即可.
解:∵二次函数的图象开口向上,
∴a>0,
∵对称轴在y轴的左边,
∴![]() <0,
<0,
∴b>0,
∵图象与y轴的交点坐标是(0,﹣2),过(1,0)点,
代入得:a+b﹣2=0,
∴a=2﹣b,b=2﹣a,
∴y=ax2+(2﹣a)x﹣2,
当x=﹣1时,y=a﹣b+c=a﹣(2﹣a)﹣2=2a﹣4,
∵b>0,
∴b=2﹣a>0,
∴a<2,
∵a>0,
∴0<a<2,
∴0<2a<4,
∴﹣4<2a﹣4<0,
∵y=a﹣b+c=a﹣(2﹣a)﹣2=2a﹣4,
∴﹣4<a﹣b+c<0,
即﹣4<m<0.
故选:D.

练习册系列答案
相关题目
【题目】某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分为100分)分成四类,并制作了如下的统计图表:
类别 | 成绩 | 频数 |
甲 | 60≤m<70 | 5 |
乙 | 70≤m<80 | a |
丙 | 80≤m<90 | 10 |
丁 | 90≤m≤100 | 5 |

根据图表信息,回答下列问题:
(1)该班共有学生________人;表中a=________;
(2)将丁类的五名学生分别记为A、B、C、D、E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方式求B一定能参加决赛的概率.