题目内容
下列说法错误的是( )
A、要使表达式
| ||||||||
B、满足不等式-
| ||||||||
C、当1,x,3分别为某个三角形的三边长时,有
| ||||||||
D、若实数a,b满足
|
分析:根据算术平方根和绝对值应不能为负数来进行解答.
解答:解:A、若表达式
•
有意义,则x-1≥0且x+1≥0,解得x≥1;故A正确;
B、满足不等式-
<x<
的整数x可取:-2、-1、0、1、2,共五个,故B正确;
C、根据三角形三边关系定理可知:3-1<x<3+1,即2<x<4;
而
=
成立,需满足的条件为x-3≥0且x-2>0,解得x≥3;
因此只有在3≤x<4时,所给的等式才成立;故C错误;
D、根据非负数的性质,得:a=4,b=2;
当2为腰长、4为底长时,2+2=4,不能构成三角形,故此种情况不成立;
当4为腰长、2为底长时,4-2<4<4+2,能构成三角形,所以这个等腰三角形的周长为:4+4+2=10;故D正确.
因此本题只有C选项的结论错误,故选C.
| x-1 |
| x+1 |
B、满足不等式-
| 5 |
| 5 |
C、根据三角形三边关系定理可知:3-1<x<3+1,即2<x<4;
而
| ||
|
| x-3 |
| x-2 |
因此只有在3≤x<4时,所给的等式才成立;故C错误;
D、根据非负数的性质,得:a=4,b=2;
当2为腰长、4为底长时,2+2=4,不能构成三角形,故此种情况不成立;
当4为腰长、2为底长时,4-2<4<4+2,能构成三角形,所以这个等腰三角形的周长为:4+4+2=10;故D正确.
因此本题只有C选项的结论错误,故选C.
点评:本题考查的知识点有:二次根式的定义及化简、非负数的性质、三角形三边关系定理等.本题需注意的是二次根式的双重非负性:
≥0,a≥0.
| a |

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
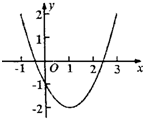 7、如图,关于抛物线y=(x-1)2-2,下列说法错误的是( )
7、如图,关于抛物线y=(x-1)2-2,下列说法错误的是( )