题目内容
若a=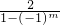
（m为正整数），且a、b互为相反数，b、c互为倒数，则ab+bm-（b-c）2m的值为
- A.0
- B.-1
- C.-2
- D.0或-2
C
分析：此题根据分数的性质可知分母不为0，可知a=1，b=-1，c=-1，代入求值即可．
解答：根据分母不为0的原则可知m为奇数，a=1，所以b=-1，c=-1，
所以ab+bm-（b-c）2m
=-1+（-1）-0
=-2，故选C．
点评：解题关键是求出a的值，进而求出b、c的值，代入即可．
分析：此题根据分数的性质可知分母不为0，可知a=1，b=-1，c=-1，代入求值即可．
解答：根据分母不为0的原则可知m为奇数，a=1，所以b=-1，c=-1，
所以ab+bm-（b-c）2m
=-1+（-1）-0
=-2，故选C．
点评：解题关键是求出a的值，进而求出b、c的值，代入即可．
练习册系列答案
相关题目