题目内容
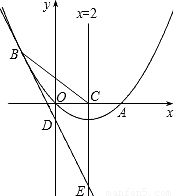
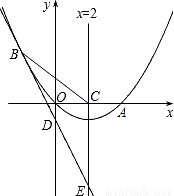
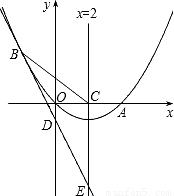
(2008•海南)如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E.(1)求m的值及该抛物线对应的函数关系式;
(2)求证:①CB=CE;②D是BE的中点;
(3)若P(x,y)是该抛物线上的一个动点,是否存在这样的点P,使得PB=PE?若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.

【答案】分析:(1)可根据直线y=-2x-1求出B点的坐标,根据A、O关于直线x=2对称,可得出A点的坐标,已知了抛物线上三点坐标即可用待定系数法求出抛物线的解析式;
(2)先求出C、B、E、D四点的坐标,
①根据C、B、E三点的坐标可求出CB,CE的长,判断它们是否相等即可;
②本题可通过构建全等三角形来求解,过B作BF⊥y轴于F,过E作EH⊥y轴于H,根据B、D、E三点坐标即可得出BF=EH,DF=DH,通过证两三角形全等即可得出BD=DE即D是BE中点的结论;
(3)若PB=PE,则P点必在线段BE的垂直平分线上即直线CD上,可求出直线CD的解析式,联立抛物线即可求出P点的坐标.
解答:(1)解:∵点B(-2,m)在直线y=-2x-1上
∴m=-2×(-2)-1=3
∴B(-2,3)
∵抛物线经过原点O和点A,对称轴为x=2
∴点A的坐标为(4,0)
设所求的抛物线对应函数关系式为y=a(x-0)(x-4)
将点B(-2,3)代入上式,得3=a(-2-0)(-2-4)
∴a=
∴所求的抛物线对应的函数关系式为y= x(x-4)
x(x-4)
即y= x2-x;
x2-x;
(2)证明:①直线y=-2x-1与y轴、直线x=2的交点坐标分别为D(0,-1)E(2,-5),
过点B作BG∥x轴,与y轴交于F、直线x=2交于G,
则BG⊥直线x=2,BG=4
在Rt△BGC中,BC=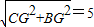
∵CE=5,
∴CB=CE=5
②过点E作EH∥x轴,交y轴于H,
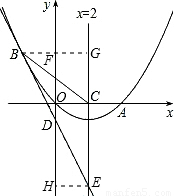
则点H的坐标为H(0,-5)
又点F、D的坐标为F(0,3)、D(0,-1)
∴FD=DH=4,BF=EH=2,∠BFD=∠EHD=90°
∴△DFB≌△DHE(SAS)
∴BD=DE
即D是BE的中点;
(3)解:存在.
由于PB=PE,∴点P在直线CD上
∴符合条件的点P是直线CD与该抛物线的交点
设直线CD对应的函数关系式为y=kx+b
将D(0,-1)C(2,0)代入,得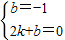 ,
,
解得k= ,b=-1
,b=-1
∴直线CD对应的函数关系式为y= x-1
x-1
∵动点P的坐标为(x, x2-x)
x2-x)
∴ x-1=
x-1= x2-x
x2-x
解得x1=3+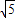 ,x2=3-
,x2=3-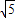
∴y1=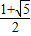 ,y2=
,y2=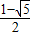
∴符合条件的点P的坐标为(3+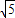 ,
,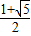 )或(3-
)或(3- ,
,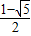 ).
).
点评:本题为二次函数综合题,考查了二次函数解析式的确定、等腰三角形的判定和性质、函数图象交点等知识.
(2)先求出C、B、E、D四点的坐标,
①根据C、B、E三点的坐标可求出CB,CE的长,判断它们是否相等即可;
②本题可通过构建全等三角形来求解,过B作BF⊥y轴于F,过E作EH⊥y轴于H,根据B、D、E三点坐标即可得出BF=EH,DF=DH,通过证两三角形全等即可得出BD=DE即D是BE中点的结论;
(3)若PB=PE,则P点必在线段BE的垂直平分线上即直线CD上,可求出直线CD的解析式,联立抛物线即可求出P点的坐标.
解答:(1)解:∵点B(-2,m)在直线y=-2x-1上
∴m=-2×(-2)-1=3
∴B(-2,3)
∵抛物线经过原点O和点A,对称轴为x=2
∴点A的坐标为(4,0)
设所求的抛物线对应函数关系式为y=a(x-0)(x-4)
将点B(-2,3)代入上式,得3=a(-2-0)(-2-4)
∴a=

∴所求的抛物线对应的函数关系式为y=
 x(x-4)
x(x-4)即y=
 x2-x;
x2-x;(2)证明:①直线y=-2x-1与y轴、直线x=2的交点坐标分别为D(0,-1)E(2,-5),
过点B作BG∥x轴,与y轴交于F、直线x=2交于G,
则BG⊥直线x=2,BG=4
在Rt△BGC中,BC=
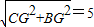
∵CE=5,
∴CB=CE=5
②过点E作EH∥x轴,交y轴于H,

则点H的坐标为H(0,-5)
又点F、D的坐标为F(0,3)、D(0,-1)
∴FD=DH=4,BF=EH=2,∠BFD=∠EHD=90°
∴△DFB≌△DHE(SAS)
∴BD=DE
即D是BE的中点;
(3)解:存在.
由于PB=PE,∴点P在直线CD上
∴符合条件的点P是直线CD与该抛物线的交点
设直线CD对应的函数关系式为y=kx+b
将D(0,-1)C(2,0)代入,得
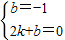 ,
,解得k=
 ,b=-1
,b=-1∴直线CD对应的函数关系式为y=
 x-1
x-1∵动点P的坐标为(x,
 x2-x)
x2-x)∴
 x-1=
x-1= x2-x
x2-x解得x1=3+
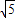 ,x2=3-
,x2=3-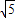
∴y1=
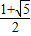 ,y2=
,y2=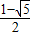
∴符合条件的点P的坐标为(3+
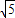 ,
,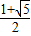 )或(3-
)或(3- ,
,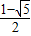 ).
).点评:本题为二次函数综合题,考查了二次函数解析式的确定、等腰三角形的判定和性质、函数图象交点等知识.

练习册系列答案
相关题目