题目内容
直线DE与△ABC的边AB相交于点D，与AC边相交于点E，下列条件中：
①DE∥BC，②∠AED=∠B，③AE•AC=AD•AB，④
=
，能使△ADE与△ABC相似的条件有（ ）
①DE∥BC，②∠AED=∠B，③AE•AC=AD•AB，④
| AE |
| AC |
| ED |
| BC |
分析：根据相似三角形的判定方法，分别进行判定即可得出答案．
解答：
解：①DE∥BC，可以根据相似三角形的判定方法中的平行线法：平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似，判断出△ADE∽△ABC，故此选项正确；
②∵∠AED=∠B，∠A=∠A，∴△AED∽△ABC，故此选项正确；
③AE•AC=AD•AB，可以变形为：
=
，又∵∠A=∠A，∴△ADE∽△ACB，故此选项正确；
④
=
，缺少夹角相等，故不能判定△ADE∽△ABC，故此选项错误；
故正确的有3个．
故选：C．
解：①DE∥BC，可以根据相似三角形的判定方法中的平行线法：平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似，判断出△ADE∽△ABC，故此选项正确；②∵∠AED=∠B，∠A=∠A，∴△AED∽△ABC，故此选项正确；
③AE•AC=AD•AB，可以变形为：
| AE |
| AB |
| AD |
| AC |
④
| AE |
| AC |
| ED |
| BC |
故正确的有3个．
故选：C．
点评：此题主要考查了相似三角形的判定，关键是掌握三角形相似的判定方法：（1）平行线法：平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似；（2）三边法：三组对应边的比相等的两个三角形相似；（3）两边及其夹角法：两组对应边的比相等且夹角对应相等的两个三角形相似；（4）两角法：有两组角对应相等的两个三角形相似．
练习册系列答案
教材全解字词句篇系列答案
相关题目
=
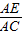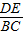中，能使△ADE与△ABC相似的条件有 个．
=
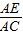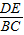中，能使△ADE与△ABC相似的条件有 个．