题目内容
直线DE与△ABC的AB边相交于点D，与AC边相交于点E，下列条件：①DE∥BC，②∠AED=∠B，③AE•AC=AD•AB，④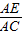
=
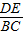中，能使△ADE与△ABC相似的条件有 个．
【答案】分析：根据相似三角形的判定定理（1）两角对应相等两三角形相似，（2）两边对应成比例且夹角相等两三角形相似；此题有个公共角∠A，所以②③能使△ADE与△ABC相似；根据平行于三角形的一边的直线截三角形的另两边或另两边的延长线所得三角形与原三角形相似，所以①正确．
解答：
解：若DE∥BC，则△ADE∽△ABC；
若∠AED=∠B，
∵∠A=∠A，
∴△ADE∽△ACB；
若AE•AC=AD•AB，
则
，
∵∠A=∠A，
∴△ADE∽△ACB；
∴能使△ADE与△ABC相似的条件有3个：是①②③．
点评：此题考查了相似三角形的判定：两角对应相等两三角形相似；两边对应成比例且夹角相等两三角形相似；平行于三角形的一边的直线截三角形的另两边或另两边的延长线所得三角形与原三角形相似．解题的关键是熟练掌握判定定理．
解答：
解：若DE∥BC，则△ADE∽△ABC；若∠AED=∠B，
∵∠A=∠A，
∴△ADE∽△ACB；
若AE•AC=AD•AB，
则
，∵∠A=∠A，
∴△ADE∽△ACB；
∴能使△ADE与△ABC相似的条件有3个：是①②③．
点评：此题考查了相似三角形的判定：两角对应相等两三角形相似；两边对应成比例且夹角相等两三角形相似；平行于三角形的一边的直线截三角形的另两边或另两边的延长线所得三角形与原三角形相似．解题的关键是熟练掌握判定定理．
练习册系列答案
相关题目
=
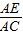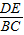中，能使△ADE与△ABC相似的条件有 个．