Question

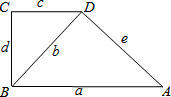
如图，在以AB为直径的半圆中，有一个边长为1的内接正方形CDEF，则以AC和BC的长为两根的一元二次方程是（   ）

A．	B．
C．	D．

Answer 1

A.

试题分析：连接AD，BD，OD，由AB为直径与四边形DCFE是正方形，即可证得△ACD∽△DCB，则可求得AC•BC=DC²=1，又由勾股定理求得AB的值，即可得AC+BC=AB，根据根与系数的关系即可求得答案．
连接AD，BD，OD，

∵AB为直径，
∴∠ADB=90°，
∵四边形DCFE是正方形，
∴DC⊥AB，
∴∠ACD=∠DCB=90°，
∴∠ADC+∠CDB=∠A+∠ADC=90°，
∴∠A=∠CDB，
∴△ACD∽△DCB，
∴，
又∵正方形CDEF的边长为1，
∵AC•BC=DC²=1，
∵AC+BC=AB，
在Rt△OCD中，，
∴，
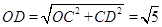∴AC+BC=AB=，
以AC和BC的长为两根的一元二次方程是