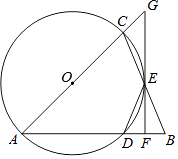题目内容
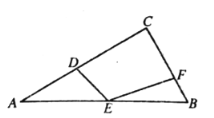
【题目】如图，在
中，
，
，点
在边
上，
，
，点
，
分别是边
，
上的动点，连接
，
，则
的最小值为_________.
【答案】
【解析】
作点D关于AB的对称点G，过点G作GF
于点F交AB于点E，此时
取得最小值. 先证出AC∥GF，得∠GEA=∠A=30
=∠DEA，可得DE=AD=4，由勾股定理求得EM的长，根据30角的直角三角形的特点以及勾股定理再求出AB，EF，即可得的值.
作点D关于AB的对称点G，过点G作GF于点F交AB于点E，此时取得最小值.
∵GF
∴∠GFB=∠C=90
∴AC∥GF
∴∠GEA=∠A=30
∴∠DEA=30
∴DE=AD=4
∴DM=2
EM=
∴AE=4
∵AC=AD+CD=4+5=9
∵ ∠A=30
∴BC=
，∠B=60
∵
∴
，
AB=
∴BE=AB-AE=
BF=
BE=，
∴EF=
=3
∴DE+EF的最小值是4+3=7.
故答案为：7.
练习册系列答案
相关题目
