题目内容
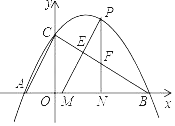
【题目】在平面直角坐标系中,已知抛物线y=x2﹣2ax+4a+2(a是常数),
(Ⅰ)若该抛物线与x轴的一个交点为(﹣1,0),求a的值及该抛物线与x轴另一交点坐标;
(Ⅱ)不论a取何实数,该抛物线都经过定点H.
①求点H的坐标;
②证明点H是所有抛物线顶点中纵坐标最大的点.
【答案】(Ⅰ)a=﹣![]() ,抛物线与x轴另一交点坐标是(0,0);(Ⅱ)①点H的坐标为(2,6);②证明见解析.
,抛物线与x轴另一交点坐标是(0,0);(Ⅱ)①点H的坐标为(2,6);②证明见解析.
【解析】
(I)根据该抛物线与x轴的一个交点为(-1,0),可以求得的值及该抛物线与x轴另一交点坐标;
(II)①根据题目中的函数解析式可以求得点H的坐标;
②将题目中的函数解析式化为顶点式,然后根据二次函数的性质即可证明点H是所有抛物线顶点中纵坐标最大的点.
(Ⅰ)∵抛物线y=x2﹣2ax+4a+2与x轴的一个交点为(﹣1,0),
∴0=(﹣1)2﹣2a×(﹣1)+4a+2,
解得,a=﹣![]() ,
,
∴y=x2+x=x(x+1),
当y=0时,得x1=0,x2=﹣1,
即抛物线与x轴另一交点坐标是(0,0);
(Ⅱ)①∵抛物线y=x2﹣2ax+4a+2=x2+2﹣2a(x﹣2),
∴不论a取何实数,该抛物线都经过定点(2,6),
即点H的坐标为(2,6);
②证明:∵抛物线y=x2﹣2ax+4a+2=(x﹣a)2﹣(a﹣2)2+6,
∴该抛物线的顶点坐标为(a,﹣(a﹣2)2+6),
则当a=2时,﹣(a﹣2)2+6取得最大值6,
即点H是所有抛物线顶点中纵坐标最大的点.

【题目】为了创建文明城市,增强学生的环保意识.随机抽取8名学生,对他们的垃圾分类投放情况进行调查,这8名学生分别标记为![]() ,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.
,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.
学生 垃圾类别 |
|
|
|
|
|
|
|
|
厨余垃圾 | √ | √ | √ | √ | √ | √ | √ | √ |
可回收垃圾 | √ | × | √ | × | × | √ | √ | √ |
有害垃圾 | × | √ | × | √ | √ | × | × | √ |
其他垃圾 | × | √ | √ | × | × | √ | √ | √ |
(1)求8名学生中至少有三类垃圾投放正确的概率;
(2)为进一步了解垃圾分类投放情况,现从8名学生里“有害垃圾”投放错误的学生中随机抽取两人接受采访,试用标记的字母列举所有可能抽取的结果.