题目内容
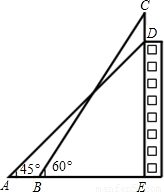
 如图,某幢大楼顶部有一块3米高的广告牌CD,小明在A点测得点D的仰角是45°,走近9米在B点测得点C的仰角是60°,且A、B、E三点在一条直线上.求这幢大楼DE的高度(
如图,某幢大楼顶部有一块3米高的广告牌CD,小明在A点测得点D的仰角是45°,走近9米在B点测得点C的仰角是60°,且A、B、E三点在一条直线上.求这幢大楼DE的高度(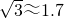 ,计算结果保留整数位).
,计算结果保留整数位).
解:设这幢大楼DE的高为x米.(1分)
由题意得CE=3+x,AB=9,
∵在Rt△AED中,∠A=45°,
∴AE=DE=x(2分)
∵在Rt△BEC中,∠CBE=60°,
∴BE=CE•cot60°(1分)
∴BE=(3+x)× ,(1分)
,(1分)
∴x-(3+x)× =9,(2分)
=9,(2分)
解得x=15+6 ≈25.(2分)
≈25.(2分)
答:这幢大楼DE的高为25米.(1分)
分析:设这幢大楼DE的高为x米,则CE=3+x,AB=9,在Rt△AED中,有∠A=45°可知AE=DE=x,在Rt△BEC中利用BE=CE•cot60°即可得出BE的值,再由AB=9可得到关于x的方程,求出x的值即可.
点评:本题考查的是解直角三角形的应用-仰角俯角问题,解答此类问题的关键是熟知锐角三角函数的定义及特殊角度的三角函数值.
由题意得CE=3+x,AB=9,
∵在Rt△AED中,∠A=45°,
∴AE=DE=x(2分)
∵在Rt△BEC中,∠CBE=60°,
∴BE=CE•cot60°(1分)
∴BE=(3+x)×
 ,(1分)
,(1分)∴x-(3+x)×
 =9,(2分)
=9,(2分)解得x=15+6
 ≈25.(2分)
≈25.(2分)答:这幢大楼DE的高为25米.(1分)
分析:设这幢大楼DE的高为x米,则CE=3+x,AB=9,在Rt△AED中,有∠A=45°可知AE=DE=x,在Rt△BEC中利用BE=CE•cot60°即可得出BE的值,再由AB=9可得到关于x的方程,求出x的值即可.
点评:本题考查的是解直角三角形的应用-仰角俯角问题,解答此类问题的关键是熟知锐角三角函数的定义及特殊角度的三角函数值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
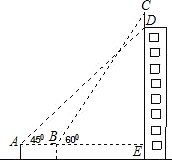 如图,某幢大楼顶部有一块广告牌CD,甲乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°和60°,且A、B、E三点在一条直线上,若BE=15米,求这块广告牌的高度.(取
如图,某幢大楼顶部有一块广告牌CD,甲乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°和60°,且A、B、E三点在一条直线上,若BE=15米,求这块广告牌的高度.(取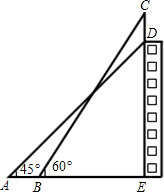 如图:某幢大楼顶部有一块广告牌CD,甲、乙两人分别在地面上相距12米的A、B两处测得点D和点C的仰角为45°和60°,且A、B、E三点在一条直线上,若BE=25m,求这块广告牌的高度.(取
如图:某幢大楼顶部有一块广告牌CD,甲、乙两人分别在地面上相距12米的A、B两处测得点D和点C的仰角为45°和60°,且A、B、E三点在一条直线上,若BE=25m,求这块广告牌的高度.(取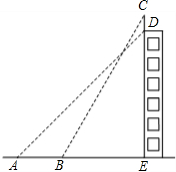 如图,某幢大楼顶部有一块3米高的广告牌CD,小明在A点测得点D的仰角是45°,走近9米在B点测得点C的仰角是60°,且A、B、E三点在一条直线上.求这幢大楼DE的高度(
如图,某幢大楼顶部有一块3米高的广告牌CD,小明在A点测得点D的仰角是45°,走近9米在B点测得点C的仰角是60°,且A、B、E三点在一条直线上.求这幢大楼DE的高度(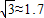 ,计算结果保留整数位).
,计算结果保留整数位).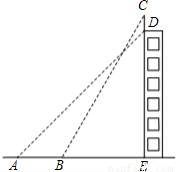
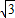 ≈1.73,计算结果精确到0.1).
≈1.73,计算结果精确到0.1).