题目内容
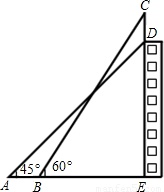
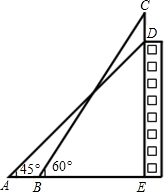如图：某幢大楼顶部有一块广告牌CD，甲、乙两人分别在地面上相距12米的A、B两处测得点D和点C的仰角为45°和60°，且A、B、E三点在一条直线上，若BE=25m，求这块广告牌的高度．（取| 3 |
分析：易得AE的值，利用45°的正切值可得DE的值，利用60°的正切值可得CE的值，相减即为广告牌的高度．
解答：解：∵BE=25m，AB=12m，
∴AE=37m，CE=BE×tan60°=25
m，
∴DE=AE×tan45°=37m，
∴CD=CE-DE≈6.3m．
答：这块广告牌的高度约为6.3m．
∴AE=37m，CE=BE×tan60°=25
| 3 |
∴DE=AE×tan45°=37m，
∴CD=CE-DE≈6.3m．
答：这块广告牌的高度约为6.3m．
点评：本题考查了解直角三角形的应用，利用锐角三角函数的知识求出线段CE和DE的长，从而根据CD=CE-DE得出问题的答案是解决本题的关键．
练习册系列答案
相关题目
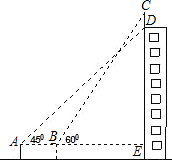如图，某幢大楼顶部有一块广告牌CD，甲乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°和60°，且A、B、E三点在一条直线上，若BE=15米，求这块广告牌的高度．（取
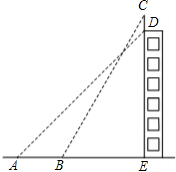如图，某幢大楼顶部有一块3米高的广告牌CD，小明在A点测得点D的仰角是45°，走近9米在B点测得点C的仰角是60°，且A、B、E三点在一条直线上．求这幢大楼DE的高度（
，计算结果保留整数位）．
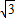≈1.73，计算结果精确到0.1）．