题目内容
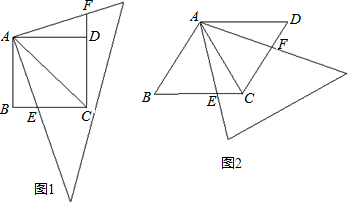
已知菱形ABCD,现将三角形纸片的一个角的顶点与A重合,适当地绕点A旋转该三角形纸片,使∠EAF=∠ABC.连接AC.(1)如图1,若∠ABC=90°,求证:CE+CF=
| 2 |
(2)如图2,若∠ABC=60°,线段CE、CF、AC三条线段的数量关系是否改变?若改变直接写出结论;若不改变请说明理由;
(3)在(2)的条件下,若菱形ABCD的周长是12,CF=1,求线段AF的长.
分析:(1)根据题干条件首先证明∠BAE=∠DAF,然后证明△ABE≌△ADF,得BE=DF,再利用正方形的性质即可得到CE+CF=
AC;
(2)根据题干条件首先证明∠BAE=∠CAF,然后证明△ABE≌△CAF,得BE=CF,再利用菱形的性质即可证明出线段CE、CF、AC三条线段的数量关系.
(3)首先根据菱形的周长求出AC的长,然后在△ACF中,AC=3,CF=1,∠ACF=60°,利用余弦定理求出AF的长.
| 2 |
(2)根据题干条件首先证明∠BAE=∠CAF,然后证明△ABE≌△CAF,得BE=CF,再利用菱形的性质即可证明出线段CE、CF、AC三条线段的数量关系.
(3)首先根据菱形的周长求出AC的长,然后在△ACF中,AC=3,CF=1,∠ACF=60°,利用余弦定理求出AF的长.
解答:(1)证明:∵∠EAF=∠ABC,
∴∠BAE=∠DAF,
∵∠B=∠D,AB=AD,
∴△ABE≌△ADF,
∴BE=DF,
∴CE+CF=2BC,
∵BC=
AC,
∴CE+CF=
AC;
(2)解:线段CE、CF、AC三条线段的数量关系改变.
∵∠ABC=60°,∠EAF=∠ABC,
∴∠BAE=∠CAF,
∵菱形ABCD,
∴AB=BC=AC,
∴△ABE≌△CAF,
∴BE=CF,
∴CE+CF=BC=AC.
故线段CE、CF、AC三条线段的数量关系改变;
(3)解:∵菱形ABCD的周长是12,
∴AB=BC=AC=3,
在△ACF中,AC=3,CF=1,∠ACF=60°,
根据余弦定理,cos60°=
,
即
=
,
解得AF=
.
∴∠BAE=∠DAF,
∵∠B=∠D,AB=AD,
∴△ABE≌△ADF,
∴BE=DF,
∴CE+CF=2BC,
∵BC=
| ||
| 2 |
∴CE+CF=
| 2 |
(2)解:线段CE、CF、AC三条线段的数量关系改变.
∵∠ABC=60°,∠EAF=∠ABC,
∴∠BAE=∠CAF,
∵菱形ABCD,
∴AB=BC=AC,
∴△ABE≌△CAF,
∴BE=CF,
∴CE+CF=BC=AC.
故线段CE、CF、AC三条线段的数量关系改变;
(3)解:∵菱形ABCD的周长是12,
∴AB=BC=AC=3,
在△ACF中,AC=3,CF=1,∠ACF=60°,
根据余弦定理,cos60°=
| AC2+ CF2-AF2 |
| 2AC•CF |
即
| 1 |
| 2 |
| 9+1-AF2 |
| 6 |
解得AF=
| 7 |
点评:本题主要考查正方形的性质和全等三角形的判定与性质的知识点,解答本题的关键是熟练掌握正方形的性质和勾股定理的应用,此题难度一般.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
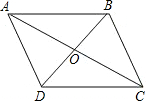 已知四边形ABCD,对角线AC、BD交于点O.现给出四个条件:
已知四边形ABCD,对角线AC、BD交于点O.现给出四个条件: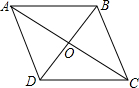 已知四边形ABCD,对角线AC、BD交于点O.现给出四个条件:AC⊥BD;②AC平分对角线BD;
已知四边形ABCD,对角线AC、BD交于点O.现给出四个条件:AC⊥BD;②AC平分对角线BD; AC;
AC;