Question

抛物线y=-

1

3

(x-2)2+1的顶点为C，已知y=-kx+3的图象经过点C，则这个一次函数图象与两坐标轴所围成的三角形面积为

 

．

Answer 1

分析：已知抛物线解析式为顶点式，可直接求出顶点C的坐标，代入y=-kx+3中求k，再求图象与两坐标轴所围成的三角形面积．

解答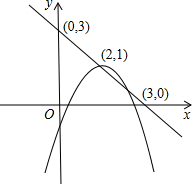：解：如图，
抛物线y=-

1

3

(x-2)2+1的顶点坐标为C（2，1），
代入y=-kx+3中，得-2k+3=1
解得k=1
∴y=-x+3
直线y=x+3与两坐标轴的交点坐标为（3，0），（0，3）
∴图象与两坐标轴所围成的三角形面积为

1

2

×3×3=

9

2

．

点评：利用二次函数的顶点式求得顶点坐标，再用待定系数法确定函数的解析式，再大体图象求得．