题目内容
△ABC中,内切圆I和边BC,CA,AB分别相切于点D,E,F,则点I是△DEF
- A.三条高的交点
- B.三个内角平分线的交点
- C.三条角平分线的交点
- D.三边垂直平分线的交点
B
分析:根据同圆的半径相等,得ID=IE=IF,该点到△DEF的三个顶点相等,则是三角形三边垂直平分线的交点.
解答:∵ID=IE=IF,I是圆心,
∴该点到△DEF的三条边的距离相等,则是三角形角平分线的交点.
故选B.
点评:熟悉外心的性质:外心是三角形三条边垂直平分线的交点,它到三角形的三个顶点的距离相等;
内心是三角形的角平分线的交点,它到三角形的三边的距离相等.
分析:根据同圆的半径相等,得ID=IE=IF,该点到△DEF的三个顶点相等,则是三角形三边垂直平分线的交点.
解答:∵ID=IE=IF,I是圆心,
∴该点到△DEF的三条边的距离相等,则是三角形角平分线的交点.
故选B.
点评:熟悉外心的性质:外心是三角形三条边垂直平分线的交点,它到三角形的三个顶点的距离相等;
内心是三角形的角平分线的交点,它到三角形的三边的距离相等.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,则∠FDE与
∠A的关系是( )
| 1 |
| 2 |
A、∠FDE+
| ||
B、∠FDE=
| ||
C、∠FDE+
| ||
| D、无法确定 |
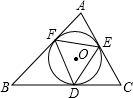 如图,△ABC中,内切圆O和边BC、CA、AB分别相切于点D、E、F,则以下四个结论中,错误的结论是( )
如图,△ABC中,内切圆O和边BC、CA、AB分别相切于点D、E、F,则以下四个结论中,错误的结论是( )| A、点O是△DEF的外心 | ||
B、∠AFE=
| ||
C、∠BOC=90°+
| ||
D、∠DFE=90°一
|
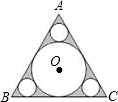 如图,已知正三角形ABC的边长为6,在△ABC中作内切圆O及三个角切圆(我们把与角两边及三角形内切圆都相切的圆叫角切圆),则△ABC的内切圆O的面积为
如图,已知正三角形ABC的边长为6,在△ABC中作内切圆O及三个角切圆(我们把与角两边及三角形内切圆都相切的圆叫角切圆),则△ABC的内切圆O的面积为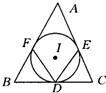 41、如图所示,△ABC中,内切圆I和边BC,CA,AB分别相切于点D,E,F,若∠FDE=70°,求∠A的度数.
41、如图所示,△ABC中,内切圆I和边BC,CA,AB分别相切于点D,E,F,若∠FDE=70°,求∠A的度数.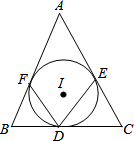 如图,△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,则∠FDE与∠A的关系是( )
如图,△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,则∠FDE与∠A的关系是( )