题目内容
 如图,双曲线
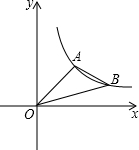
如图,双曲线 经过点A(2,2)与点B(4,m),求△AOB的面积.
经过点A(2,2)与点B(4,m),求△AOB的面积.
 解:过A、B分别作x轴的垂线,垂足分别为C、D,如图,
解:过A、B分别作x轴的垂线,垂足分别为C、D,如图,∵双曲线y=
 经过点A(2,2),
经过点A(2,2),∴k=2×2=4,
而点B(4,m)在y=
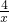 上,
上,∴4•m=4,
解得m=1,
即B点坐标为(4,1)
∴S△AOB=S△AOC+S梯形ABDC-S△BOD,
=
 OC•AC+
OC•AC+ ×(AC+BD)×CD-
×(AC+BD)×CD- ×OD×BD,
×OD×BD,=
 ×2×2+
×2×2+ ×(2+1)×(4-2)-
×(2+1)×(4-2)- ×4×1,
×4×1,=3.
分析:过A、B分别作x轴的垂线,垂足分别为C、D,把点A(2,2)代入双曲线y=
 确定k的值,再把点B(4,m)代入双曲线y=
确定k的值,再把点B(4,m)代入双曲线y= 确定点B的坐标,根据S△AOB=S△AOC+S梯形ABDC-S△BOD进行计算即可.
确定点B的坐标,根据S△AOB=S△AOC+S梯形ABDC-S△BOD进行计算即可.点评:本题考查了反比例函数,利用坐标表示线段的长,以及利用规则的几何图形的面积计算不规则的图形面积.只要点在图象上,则点的横纵坐标满足图象的解析式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 经过点A(2,2)与点B(4,m),求△AOB的面积.
经过点A(2,2)与点B(4,m),求△AOB的面积.
 经过点A(2,2)与点B(4,m),则△AOB的面积为( )
经过点A(2,2)与点B(4,m),则△AOB的面积为( )
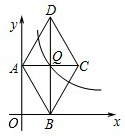 已知:如图,双曲线
已知:如图,双曲线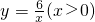 经过点Q(2,n).
经过点Q(2,n). 经过点Q(2,n).
经过点Q(2,n).