题目内容
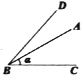
【题目】如图,在△ABC 中，AB=AC,∠BAC 的角平分线与∠ABC 的角平分线交于点 D,若∠ADB=130°，∠C=（ ）
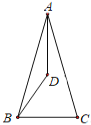
A.50°B.65°C.80°D.100°
【答案】C
【解析】
本题考察的是角平分线的定义与三角形内角和的运用，由三角形内角和为180°，∠ADB=130°可知，∠DAB与∠DBA的和，再由角平分线的定义可知，∠CAB与∠CBA的和，再利用三角形内角和为180°可求∠C
∵在△ABD中，∠ADB=130°，∴∠DAB+∠DBA=180°-∠ADB=50°，又∵DA与DB分别是∠ABC与∠BAC 的角平分线，∴∠CAB+∠CBA=2（∠DAB+∠DBA）=100°，∴∠C=180°-（∠CAB+∠CBA）=80°
练习册系列答案
百年学典课时学练测系列答案
相关题目
【题目】如图，点A是一次函数y=﹣
x+
的图象与反比例函数y=
（m＞0）的图象的一个交点，AB⊥x轴，垂足为B，且AB=．
（1）求这个反比例函数的解析式；
（2）当1＜x＜4，求反比例函数y=的取值范围．
