题目内容
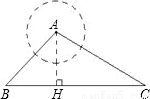
如图,点A是一个半径为300米的圆形森林公园的中心,在森林公园附近有B、C两个村庄,现要在B、C两村庄之间修一条长为1000米的笔直公路将两村连通.经测得∠ABC=45°,∠ACB=30°,问此公路是否会穿过森林公园?请通过计算进行说明.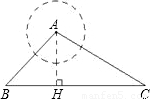
【答案】分析:根据已知求得AH的长,将其与300进行比较,若大于300则不会穿过,否则会穿过.
解答:解:不会穿过森林公园.
因为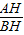 =tan45°=1,所以BH=AH.
=tan45°=1,所以BH=AH.
又因为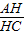 =tan30°=
=tan30°=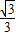 ,所以HC=
,所以HC=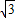 AH.
AH.
所以BC=BH+HC=AH+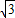 AH=(
AH=(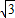 +1)AH.
+1)AH.
又因为BC=1000,所以( +1)AH=1000.
+1)AH=1000.
所以AH=500(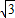 -1).
-1).
而500(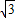 -1)>300,
-1)>300,
故此公路不会穿过森林公园.
点评:解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
解答:解:不会穿过森林公园.
因为
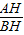 =tan45°=1,所以BH=AH.
=tan45°=1,所以BH=AH.又因为
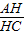 =tan30°=
=tan30°=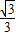 ,所以HC=
,所以HC=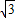 AH.
AH.所以BC=BH+HC=AH+
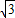 AH=(
AH=(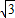 +1)AH.
+1)AH.又因为BC=1000,所以(
 +1)AH=1000.
+1)AH=1000.所以AH=500(
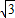 -1).
-1).而500(
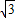 -1)>300,
-1)>300,故此公路不会穿过森林公园.
点评:解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
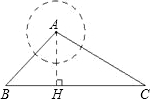 如图,点A是一个半径为300米的圆形森林公园的中心,在森林公园附近有B、C两个村庄,现要在B、C两村庄之间修一条长为1000米的笔直公路将两村连通.经测得∠ABC=45°,∠ACB=30°,问此公路是否会穿过森林公园?请通过计算进行说明.
如图,点A是一个半径为300米的圆形森林公园的中心,在森林公园附近有B、C两个村庄,现要在B、C两村庄之间修一条长为1000米的笔直公路将两村连通.经测得∠ABC=45°,∠ACB=30°,问此公路是否会穿过森林公园?请通过计算进行说明.