题目内容
已知:如图,⊙O的直径为10,弦AC=8,点B在圆周上运动(与A、C两点不重合),连接BC、BA,过点C作CD⊥AB于D、设CB的长为x,CD的长为y.(1)求y关于x的函数关系式;当以BC为直径的圆与AC相切时,求y的值;
(2)在点B运动的过程中,以CD为直径的圆与⊙O有几种位置关系,并求出不同位置时y的取值范围;
(3)在点B运动的过程中,如果过B作BE⊥AC于E,那么以BE为直径的圆与⊙O能内切吗?若不能,说明理由;若能,求出BE的长.

分析:(1)∵直径为10,弦AC=8,CD⊥AB,CB的长为x,CD的长为y,∴y=
x,当以CB为直径的圆与AC相切时,点B与点M重合,即可求解;
(2)①当CB=CA=8时,两圆内切,②当CB≠8时,两圆相交;讨论后即可得出答案;
(3)假设以BE为直径的圆与⊙O可以内切,看能否求出BE即可;
| 4 |
| 5 |
(2)①当CB=CA=8时,两圆内切,②当CB≠8时,两圆相交;讨论后即可得出答案;
(3)假设以BE为直径的圆与⊙O可以内切,看能否求出BE即可;
解答: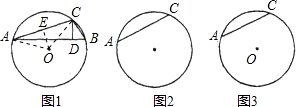 解:(1)如图1,连接OA、OC、.过圆心O作OE⊥AC于点E.
解:(1)如图1,连接OA、OC、.过圆心O作OE⊥AC于点E.
∵直径为10,弦AC=8,
∴OC=5,CE=8,∠AOE=∠COE.
又∵∠ABC=
∠AOC=∠COE,CD⊥AB,CB的长为x,
CD的长为y,
∴y=
x,当以CB为直径的圆与AC相切时,点B与点M重合,
此时,x=6,y=4.8;
(2)以DC为直径的圆与⊙O的位置关系是相交或内切,
①当CB=CA=8时,两圆内切,y=
×8=6.4;
②当CB≠8时,两圆相交,0<y≤8,且y≠6.4.
(3)以BE为直径的圆与⊙O可以内切,
∵BE⊥AC,CD⊥AB,
∴BE=5-3=2或BE=5+3=8.
 解:(1)如图1,连接OA、OC、.过圆心O作OE⊥AC于点E.
解:(1)如图1,连接OA、OC、.过圆心O作OE⊥AC于点E.∵直径为10,弦AC=8,
∴OC=5,CE=8,∠AOE=∠COE.
又∵∠ABC=
| 1 |
| 2 |
CD的长为y,
∴y=
| 4 |
| 5 |
此时,x=6,y=4.8;
(2)以DC为直径的圆与⊙O的位置关系是相交或内切,
①当CB=CA=8时,两圆内切,y=
| 4 |
| 5 |
②当CB≠8时,两圆相交,0<y≤8,且y≠6.4.
(3)以BE为直径的圆与⊙O可以内切,
∵BE⊥AC,CD⊥AB,
∴BE=5-3=2或BE=5+3=8.
点评:本题考查了一次函数与圆与圆的位置关系,难度较大,关键是分类讨论两圆的位置关系.

练习册系列答案
相关题目
 窗户B,这时PA平分∠BPC.若点P到大楼的水平距离PC为10米.
窗户B,这时PA平分∠BPC.若点P到大楼的水平距离PC为10米. (2013•南通一模)已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
(2013•南通一模)已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
 已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12. 已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.