题目内容
 已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
(1)求b的值;
(2)若点P是线段AB中垂线上的点,是否存在这样的点P,使△PBC成为直角三角形?若存在,试直接写出所有符合条件的点P的坐标;若不存在,试说明理由;
(3)点Q为线段AB上一个动点(点Q与点A、B不重合),QE∥AC,交BC于点E,以QE为边,在点B的异侧作正方形QEFG.设AQ=m,△ABC与正方形QEFG的重叠部分的面积为S,试求S与m之间的函数关系式,并写出m的取值范围.
解:(1)由题意得:B(- ,0),C(0,b)
,0),C(0,b)
∴OB= ,OC=b
,OC=b
∵AO=BO
∴A(b,0).∴OA=b,AB=b+ =
= b.
b.
∵S△ABC= AB•OC=12
AB•OC=12
∴ ×
× b•b=12
b•b=12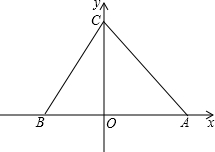
解得:b1=4,b2=-4(舍去)
∴b=4
(2)AB的中垂线是x=1,
当A是直角△BCP的直角顶点时,设BP的解析式是:y=- x+c,
x+c,
把B的坐标代入得:1+c=0,解得:c=-1,
则BP的解析式是:y=- x-1,当x=1时,y=-
x-1,当x=1时,y=- ,
,
则P的坐标是(1,- );
);
同理,当C是直角顶点时求得P的坐标是(1, );
);
当P是直角顶点时,BC= =2
=2 ,
,
BC的中点的坐标是(-1,2),
设P的坐标是(1,x),则(x-2)2+(1+1)2=( )2,
)2,
解得:x=1或3,
则P的坐标是(1,1)或(1,3).
总之,P的坐标是:P1(1,1),P2(1,3),P4(1, ),P3(1,-
),P3(1,- ).
).
(3)如图,设正方形QEFG与AC相交于点M.
∵B(-2,0),A(4,0)
∴AB=6
在Rt△AOC中AC= =4
=4
∵EQ∥AC
∴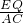 =
=
∴EQ=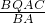 =
=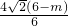 =
=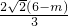 .
.
∵EQ∥AC
∴∠AMQ=∠EQM=90°∠MAQ=45°
∴△QMA为等腰直角三角形
∴QM= AQ=
AQ= m
m
当QM=QG时,正方形QEFG的边FG恰好与AC共线.
此时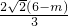 =
= m,
m,
解得:m=
当0<m≤ 时,S=QE•QM=
时,S=QE•QM=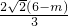 •
• m=-
m=- m2+4m.
m2+4m.
当 <m<6时,S=QE2=[
<m<6时,S=QE2=[
 (6-m)】2=
(6-m)】2= (m-6)2.
(m-6)2.
∴S与m之间的函数关系式为S=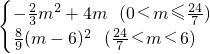 .
.
分析:(1)根据△ABC的面积是12,即可得到一个关于b的方程,解方程求得b的值;
(2)线段AB中垂线的解析式是y=1,然后分A、B、P是直角顶点三种情况进行讨论即可求得;
(3)在Rt△AOC中利用勾股定理求得AC的长度,然后根据平行线分线段成比例定理利用m表示出EQ的长度,然后分0<m≤ 和
和 <m<6两种情况求得.
<m<6两种情况求得.
点评:本题考查了一次函数与直角三角形的性质、正方形的性质、平行线分线段成比例定理的综合应用,正确分类讨论是关键.
 ,0),C(0,b)
,0),C(0,b)∴OB=
 ,OC=b
,OC=b∵AO=BO
∴A(b,0).∴OA=b,AB=b+
 =
= b.
b.∵S△ABC=
 AB•OC=12
AB•OC=12∴
 ×
× b•b=12
b•b=12
解得:b1=4,b2=-4(舍去)
∴b=4
(2)AB的中垂线是x=1,
当A是直角△BCP的直角顶点时,设BP的解析式是:y=-
 x+c,
x+c,把B的坐标代入得:1+c=0,解得:c=-1,
则BP的解析式是:y=-
 x-1,当x=1时,y=-
x-1,当x=1时,y=- ,
,则P的坐标是(1,-
 );
);同理,当C是直角顶点时求得P的坐标是(1,
 );
);当P是直角顶点时,BC=
 =2
=2 ,
,BC的中点的坐标是(-1,2),
设P的坐标是(1,x),则(x-2)2+(1+1)2=(
 )2,
)2,解得:x=1或3,
则P的坐标是(1,1)或(1,3).
总之,P的坐标是:P1(1,1),P2(1,3),P4(1,
 ),P3(1,-
),P3(1,- ).
).(3)如图,设正方形QEFG与AC相交于点M.
∵B(-2,0),A(4,0)
∴AB=6
在Rt△AOC中AC=
 =4
=4
∵EQ∥AC
∴
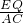 =
=
∴EQ=
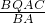 =
=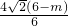 =
=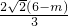 .
.∵EQ∥AC
∴∠AMQ=∠EQM=90°∠MAQ=45°
∴△QMA为等腰直角三角形
∴QM=
 AQ=
AQ= m
m当QM=QG时,正方形QEFG的边FG恰好与AC共线.
此时
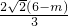 =
= m,
m,解得:m=

当0<m≤
 时,S=QE•QM=
时,S=QE•QM=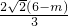 •
• m=-
m=- m2+4m.
m2+4m.当
 <m<6时,S=QE2=[
<m<6时,S=QE2=[
 (6-m)】2=
(6-m)】2= (m-6)2.
(m-6)2.∴S与m之间的函数关系式为S=
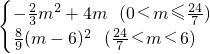 .
.分析:(1)根据△ABC的面积是12,即可得到一个关于b的方程,解方程求得b的值;
(2)线段AB中垂线的解析式是y=1,然后分A、B、P是直角顶点三种情况进行讨论即可求得;
(3)在Rt△AOC中利用勾股定理求得AC的长度,然后根据平行线分线段成比例定理利用m表示出EQ的长度,然后分0<m≤
 和
和 <m<6两种情况求得.
<m<6两种情况求得.点评:本题考查了一次函数与直角三角形的性质、正方形的性质、平行线分线段成比例定理的综合应用,正确分类讨论是关键.

练习册系列答案
相关题目
 窗户B,这时PA平分∠BPC.若点P到大楼的水平距离PC为10米.
窗户B,这时PA平分∠BPC.若点P到大楼的水平距离PC为10米. (2013•南通一模)已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
(2013•南通一模)已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
 已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.