题目内容
17、Rt△ABC中，斜边AB=1，则AB2+BC2+AC2的值是
2
．分析：先画图，再利用勾股定理可求BC2+AC2的值，从而易求AB2+BC2+AC2的值．
解答：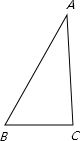
解：如右图所示，
在Rt△ABC中，AB2=BC2+AC2，
又∵AB=1，
∴BC2+AC2，=AB2=1，
∴AB2+BC2+AC2=1+1=2．
故答案是2．
解：如右图所示，在Rt△ABC中，AB2=BC2+AC2，
又∵AB=1，
∴BC2+AC2，=AB2=1，
∴AB2+BC2+AC2=1+1=2．
故答案是2．
点评：本题考查了勾股定理，直角三角形中，两直角边的平方和等于斜边的平方．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
