题目内容
已知在Rt△ABC中，斜边AB=5，BC=3，以点A为旋转中心，旋转这个三角形至△AB'C'的位置，那么当点C'落在直线AB上时，BB'=分析：分两种情况：①点C′在线段AB上；②点C′在线段AB的延长线上；利用勾股定理求解即可．
解答：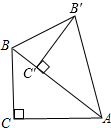
解：①当点C′在线段AB上；
∵AB=5，BC=3，
∴AC′=4
∵以点A为旋转中心，旋转这个三角形至△AB'C'的位置，
∴BC′=1，B′C′=3，
∴BB′=
；
②当点C′在线段AB的延长线上；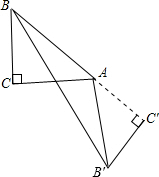
∵AB=5，BC=3，
∴AC′=4
∵以点A为旋转中心，旋转这个三角形至△AB'C'的位置，
∴BC′=9，B′C′=3，
∴BB′=3
；
故答案为
或3
．
解：①当点C′在线段AB上；∵AB=5，BC=3，
∴AC′=4
∵以点A为旋转中心，旋转这个三角形至△AB'C'的位置，
∴BC′=1，B′C′=3，
∴BB′=
| 10 |
②当点C′在线段AB的延长线上；
∵AB=5，BC=3，
∴AC′=4
∵以点A为旋转中心，旋转这个三角形至△AB'C'的位置，
∴BC′=9，B′C′=3，
∴BB′=3
| 10 |
故答案为
| 10 |
| 10 |
点评：本题考查了旋转的性质以及勾股定理，要注意分类讨论思想，是解题的关键．
练习册系列答案
相关题目
如图，已知在Rt△ABC中，∠ACB=90°，AB=4，分别以AC，BC为直径作半圆，面积分别记为S1，S2，则S1+S2的值等于（ ）
（1）已知在Rt△ABC中，∠C=90°，sinA=