题目内容
 学校围墙边有一个直角三角形的花圃(如图1所示的Rt△ABC),其中斜边AB借助围墙,两条直角边AC和BC用铁栅栏围成,已知AB=10米,AC=8米.
学校围墙边有一个直角三角形的花圃(如图1所示的Rt△ABC),其中斜边AB借助围墙,两条直角边AC和BC用铁栅栏围成,已知AB=10米,AC=8米.
(1)求这个直角三角形花圃的面积.
(2)现在要将这个直角三角形花圃扩充成等腰三角形,设计方案要求斜边AB不变,只能延长两条直角边中的一条.图2是已经设计好的一种方案:延长BC到P,使PA=PB,把花圃扩充成等腰△PAB.设CP的长为x米,请你求出x的值,并计算△PAB的面积.
(3)请你仿照(2)中的方法,设计符合(2)中要求的方案,在下列各图中
画出扩充后的等腰三角形花圃△PAB的示意图,并直接写出△PAB的面积.

 解:(1)在Rt△ABC中,
解:(1)在Rt△ABC中,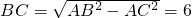 (米),
(米),∴S△ABC=
 AC•BC=
AC•BC= ×8×6=24(米2);
×8×6=24(米2);(2)在Rt△APC中,AP2=PC2+AC2
即(6+x)2=82+x2,
解得
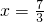
∴S△PAB=
 ×(
×( +6)×8=
+6)×8= =33
=33 (米2);
(米2);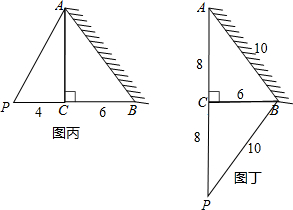
(3)如图甲,
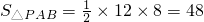 (米2);
(米2);如图乙,
 (米2);
(米2);如图丙,
 (米2);
(米2); 如图丁,
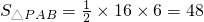 (米2)
(米2)分析:(1)利用勾股定理得出BC的长,进而得出三角形花圃的面积;
(2)利用勾股定理AP2=PC2+AC2即(6+x)2=82+x2,得出三角形的高,进而得出面积;
(3)分别利用图形得出甲,乙,丙,丁4个图形面积,即可得出答案.
点评:此题主要考查了应用与设计作图和勾股定理的应用,利用已知得出三角形的底与高是解题关键.

练习册系列答案
相关题目
 学校围墙边有一个直角三角形的花圃(如图1所示的Rt△ABC),其中斜边AB借助围墙,两条直角边AC和BC用铁栅栏围成,已知AB=10米,AC=8米.
学校围墙边有一个直角三角形的花圃(如图1所示的Rt△ABC),其中斜边AB借助围墙,两条直角边AC和BC用铁栅栏围成,已知AB=10米,AC=8米.