题目内容
己知点P(2,3)是反比例函数y= 图象上的点.
图象上的点.
(1)求过点P且与反比例函数y= 图象只有一个公共点的直线的解析式;
图象只有一个公共点的直线的解析式;
(2)Q是反比例函数y= 图象在第三象限这一分支上的动点,过点Q作直线使其与反比例函数y=
图象在第三象限这一分支上的动点,过点Q作直线使其与反比例函数y= 图象只有一个公共点,且与x轴、y轴分别交于C、D两点,设(1)中求得的一直线与x轴、y轴分别交于A、B两点.
图象只有一个公共点,且与x轴、y轴分别交于C、D两点,设(1)中求得的一直线与x轴、y轴分别交于A、B两点.
①试判断AD、BC的位置关系;
②探索当四边形ABCD面积最小时,四边形ABCD的形状.
(1)解:将P的坐标代入反比例解析式得:3=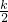 ,即k=6,
,即k=6,
则反比例函数解析式为y=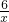 ,
,
显然直线x=2与直线y=3与反比例函数图象只有一个交点,满足题意;
设第三条直线解析式为y=ax+b,
∵把P(2,3)代入得:3=2k+b,
即b=3-2k,
∴y=kx+3-2k,
联立直线与反比例解析式得:
 ,
,
消去y整理得:kx2+(3-2k)x-6=0,
由题意得到方程有两个相等的实数根,得到△=(3-2k)2+24k=(2k+3)2=0,
解得:k=- ,
,
故满足题意的第三条直线为y=- x+6;
x+6;
(2)①由(1)求出的直线y=- x+6,令x=0,得到y=6;令y=0,得到x=4,
x+6,令x=0,得到y=6;令y=0,得到x=4,
则A(4,0),B(0,6),即OA=4,OB=6,
设直线CD的解析式为y=mx+n,
则 只有一个解,
只有一个解,
消去y整理得:mx2+nx-6=0,
△=n2+24m=0,
- =24,
=24,
OC•OD=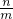 •(-n)=24=OA•OB,即
•(-n)=24=OA•OB,即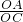 =
=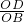 ,
,
AD∥BC;
②设OC=t,则OD=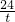 ,
,
S四边形ABCD=S△BCD+S△BDA= ×(6+
×(6+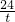 )×r+
)×r+ ×(6+
×(6+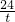 )×4
)×4
=3t+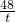 +24
+24
=3(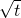 -
-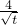 )2+48,
)2+48,
则当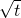 -
-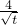 =0,即t=4时,四边形ABCD面积最小,
=0,即t=4时,四边形ABCD面积最小,
此时OA=OC=4,OB=OD=6,又AC⊥BD,
故四边形ABCD为菱形.
分析:(1)把P的坐标代入即可求出反比例函数的解析式,得出直线x=2和直线y=3符合题意,设第三条直线解析式为y=ax+b,把P(2,3)代入得出y=kx+3-2k,联立直线与反比例解析式得出方程kx2+(3-2k)x-6=0,根据根与系数的关系求出k,即可求出直线的解析式;
(2))①由(1)求出的直线y=- x+6,求出A和B的坐标,得出OA=4,OB=6,设直线CD的解析式为y=mx+n,得出方程组
x+6,求出A和B的坐标,得出OA=4,OB=6,设直线CD的解析式为y=mx+n,得出方程组 ,消去y整理后求出-
,消去y整理后求出- =24,求出OC•OD=OA•OB,得出
=24,求出OC•OD=OA•OB,得出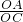 =
=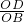 ,即可得出平行;②设OC=t,则OD=
,即可得出平行;②设OC=t,则OD= ,根据S四边形ABCD=S△BCD+S△BDA得出S=3t+
,根据S四边形ABCD=S△BCD+S△BDA得出S=3t+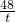 +24,化成顶点式即可求出t,根据菱形的判定推出即可.
+24,化成顶点式即可求出t,根据菱形的判定推出即可.
点评:本题综合考查了三角形的面积,反比例函数的解析式,平行线的性质和判定,菱形的判定,根的判别式,方程组等知识点,主要考查学生综合运用性质进行计算的能力,本题综合性比较强,难度偏大,对学生提出较高的要求.
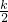 ,即k=6,
,即k=6,则反比例函数解析式为y=
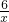 ,
,显然直线x=2与直线y=3与反比例函数图象只有一个交点,满足题意;
设第三条直线解析式为y=ax+b,
∵把P(2,3)代入得:3=2k+b,
即b=3-2k,
∴y=kx+3-2k,
联立直线与反比例解析式得:
 ,
,消去y整理得:kx2+(3-2k)x-6=0,
由题意得到方程有两个相等的实数根,得到△=(3-2k)2+24k=(2k+3)2=0,
解得:k=-
 ,
,故满足题意的第三条直线为y=-
 x+6;
x+6;(2)①由(1)求出的直线y=-
 x+6,令x=0,得到y=6;令y=0,得到x=4,
x+6,令x=0,得到y=6;令y=0,得到x=4,则A(4,0),B(0,6),即OA=4,OB=6,
设直线CD的解析式为y=mx+n,
则
 只有一个解,
只有一个解,消去y整理得:mx2+nx-6=0,
△=n2+24m=0,
-
 =24,
=24,OC•OD=
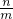 •(-n)=24=OA•OB,即
•(-n)=24=OA•OB,即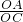 =
=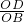 ,
,AD∥BC;
②设OC=t,则OD=
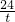 ,
,S四边形ABCD=S△BCD+S△BDA=
 ×(6+
×(6+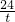 )×r+
)×r+ ×(6+
×(6+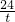 )×4
)×4=3t+
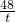 +24
+24=3(
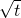 -
-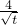 )2+48,
)2+48,则当
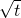 -
-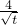 =0,即t=4时,四边形ABCD面积最小,
=0,即t=4时,四边形ABCD面积最小,此时OA=OC=4,OB=OD=6,又AC⊥BD,
故四边形ABCD为菱形.
分析:(1)把P的坐标代入即可求出反比例函数的解析式,得出直线x=2和直线y=3符合题意,设第三条直线解析式为y=ax+b,把P(2,3)代入得出y=kx+3-2k,联立直线与反比例解析式得出方程kx2+(3-2k)x-6=0,根据根与系数的关系求出k,即可求出直线的解析式;
(2))①由(1)求出的直线y=-
 x+6,求出A和B的坐标,得出OA=4,OB=6,设直线CD的解析式为y=mx+n,得出方程组
x+6,求出A和B的坐标,得出OA=4,OB=6,设直线CD的解析式为y=mx+n,得出方程组 ,消去y整理后求出-
,消去y整理后求出- =24,求出OC•OD=OA•OB,得出
=24,求出OC•OD=OA•OB,得出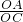 =
=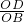 ,即可得出平行;②设OC=t,则OD=
,即可得出平行;②设OC=t,则OD= ,根据S四边形ABCD=S△BCD+S△BDA得出S=3t+
,根据S四边形ABCD=S△BCD+S△BDA得出S=3t+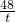 +24,化成顶点式即可求出t,根据菱形的判定推出即可.
+24,化成顶点式即可求出t,根据菱形的判定推出即可.点评:本题综合考查了三角形的面积,反比例函数的解析式,平行线的性质和判定,菱形的判定,根的判别式,方程组等知识点,主要考查学生综合运用性质进行计算的能力,本题综合性比较强,难度偏大,对学生提出较高的要求.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
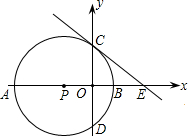 D,其中A(-3,0),B(1,0).过点C作⊙P的切线交x轴于点E.
D,其中A(-3,0),B(1,0).过点C作⊙P的切线交x轴于点E. 图象上的点.
图象上的点.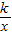 图象只有一个公共点的直线的解析式;
图象只有一个公共点的直线的解析式;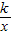 图象在第三象限这一分支上的动点,过点Q作直线使其与反比例函数y=
图象在第三象限这一分支上的动点,过点Q作直线使其与反比例函数y=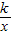 图象只有一个公共点,且与x轴、y轴分别交于C、D两点,设(1)中求得的一直线与x轴、y轴分别交于A、B两点.
图象只有一个公共点,且与x轴、y轴分别交于C、D两点,设(1)中求得的一直线与x轴、y轴分别交于A、B两点.