题目内容
按语句画图。
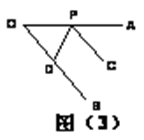
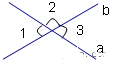
(1)作锐角∠AOB;
(2)作射线OC⊥OA,OD⊥OB;
(3)判断∠AOB与∠COD的关系,并且说明理由
(1)作锐角∠AOB;
(2)作射线OC⊥OA,OD⊥OB;
(3)判断∠AOB与∠COD的关系,并且说明理由
(1)略(2分)(2)略(2分)(3)互补(2分)
分析:(1)根据锐角的定义作一个大于0°小于90°的角即可;
(2)分别根据垂直的概念画出图形即可,注意分情况作图;
(3)根据周角和垂直的定义和余角的性质即可得出∠AOB与∠COD的关系.
解答:答:(1)作锐角∠AOB如下:
(2)作射线OC⊥OA,OD⊥OB如下:
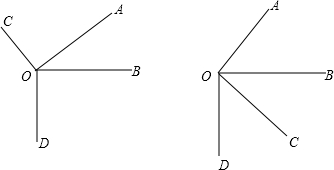
(3)互补或相等.
理由:①∠AOB+∠COD=360°-90°-90°=180°,即∠AOB与∠COD互补;
②∵∠AOB+∠BOC=∠COD+∠BOC=90°,∴∠AOB=∠COD,
即∠AOB与∠COD相等.故∠AOB与∠COD互补或相等.
点评:本题考查了角的作图,垂线的画法,周角定义和余角的性质,难度不大.
(2)分别根据垂直的概念画出图形即可,注意分情况作图;
(3)根据周角和垂直的定义和余角的性质即可得出∠AOB与∠COD的关系.
解答:答:(1)作锐角∠AOB如下:

(2)作射线OC⊥OA,OD⊥OB如下:

(3)互补或相等.
理由:①∠AOB+∠COD=360°-90°-90°=180°,即∠AOB与∠COD互补;
②∵∠AOB+∠BOC=∠COD+∠BOC=90°,∴∠AOB=∠COD,
即∠AOB与∠COD相等.故∠AOB与∠COD互补或相等.
点评:本题考查了角的作图,垂线的画法,周角定义和余角的性质,难度不大.

练习册系列答案
相关题目