题目内容
一辆邮政车自A城驶往B城,沿途有n个车站(包括起点A和终点B),该车在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该车站的邮包一个,还要装上该车站发给后面行程中每个车站的邮包一个.邮车在第1个车站 (A站)启程时要装上该站发给后面行程中每个车站的邮包(n-1)个,邮车上邮包总数是(n-1)个;邮车到第2个车站,卸下邮包1个,启程时要装上该站发给后面行程中每个车站的邮包(n-2)个,邮车上邮包总数是______(个).
(1)邮车到第4个车站,启程时计算出邮车上邮包个数;
(2)邮车到第x个车站,启程时邮车上邮包总数是多少(用x,n表示)?
(3)当n=18,x=9时,求出邮车上邮包的个数.
解:(1)在第1个车站(x=1)启程时邮包的总个数:n-1;
在第2个车站(x=2)启程时邮包的总个数:n-1-1+n-2=2(n-2);
在第3个车站(x=3)启程时邮包的总个数:2(n-2)-2+n-3=3(n-3);
在第4个车站(x=4)启程时邮包的总个数:3(n-3)-3+n-4=4(n-4);
…
在第4个车站启程时邮包的总个数x(n-x);
故邮车到第4个车站,启程时计算出邮车上邮包个数为:4(n-4);
(2)由(1)可得:邮车到第x个车站,启程时邮车上邮包总数是x(n-x)个.
(3)当n=18,x=9时,x(n-x)=81,
故当n=18,x=9时,邮车上邮包的个数是81个.
分析:(1)写出前3站邮包的数量,即可得出第4站邮包的数量;
(2)根据前4站邮包的数量,总结出一般规律,可得第x个车站,启程时邮车上邮包总数.
(3)将n=18,x=9代入(2)的关系式,可得出答案.
点评:本题考查了列代数式的知识,解答本题的关键是求出前几站出发时邮包的数量,总结出一般规律,有一定难度.
在第2个车站(x=2)启程时邮包的总个数:n-1-1+n-2=2(n-2);
在第3个车站(x=3)启程时邮包的总个数:2(n-2)-2+n-3=3(n-3);
在第4个车站(x=4)启程时邮包的总个数:3(n-3)-3+n-4=4(n-4);
…
在第4个车站启程时邮包的总个数x(n-x);
故邮车到第4个车站,启程时计算出邮车上邮包个数为:4(n-4);
(2)由(1)可得:邮车到第x个车站,启程时邮车上邮包总数是x(n-x)个.
(3)当n=18,x=9时,x(n-x)=81,
故当n=18,x=9时,邮车上邮包的个数是81个.
分析:(1)写出前3站邮包的数量,即可得出第4站邮包的数量;
(2)根据前4站邮包的数量,总结出一般规律,可得第x个车站,启程时邮车上邮包总数.
(3)将n=18,x=9代入(2)的关系式,可得出答案.
点评:本题考查了列代数式的知识,解答本题的关键是求出前几站出发时邮包的数量,总结出一般规律,有一定难度.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
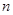 个车站(包括起点A和终点B),该车在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该车站的邮包一个,还要装上该车站发给后面行程中每个车站的邮包一个.邮车在第1个车站 (A站)启程时要装上该站发给后面行程中每个车站的邮包
个车站(包括起点A和终点B),该车在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该车站的邮包一个,还要装上该车站发给后面行程中每个车站的邮包一个.邮车在第1个车站 (A站)启程时要装上该站发给后面行程中每个车站的邮包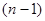 个,邮车上邮包总数是
个,邮车上邮包总数是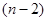 个,邮车上邮包总数是 (个).
个,邮车上邮包总数是 (个).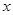 个车站,启程时邮车上邮包总数是多少(用
个车站,启程时邮车上邮包总数是多少(用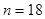 ,
,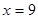 时,求出邮车上邮包的个数.
时,求出邮车上邮包的个数.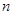 个车站(包括起点A和终点B),该车在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该车站的邮包一个,还要装上该车站发给后面行程中每个车站的邮包一个.邮车在第1个车站 (A站)启程时要装上该站发给后面行程中每个车站的邮包
个车站(包括起点A和终点B),该车在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该车站的邮包一个,还要装上该车站发给后面行程中每个车站的邮包一个.邮车在第1个车站 (A站)启程时要装上该站发给后面行程中每个车站的邮包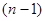 个,邮车上邮包总数是
个,邮车上邮包总数是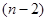 个,邮车上邮包总数是 (个).
个,邮车上邮包总数是 (个).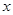 个车站,启程时邮车上邮包总数是多少(用
个车站,启程时邮车上邮包总数是多少(用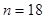 ,
,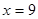 时,求出邮车上邮包的个数.
时,求出邮车上邮包的个数.