题目内容
26、一辆邮政车自A城驶往B城,沿途有n个车站(包括起点A和终点B),行驶时需要在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该车站的邮包一个,还要装上该站发给后面行程中每个车站的邮包一个.例如,当邮车停靠在第x个车站时,需要卸下已经通过的(x-1) 个车站发给该站的邮包(x-1)个,还要装上后面行程中要停靠的(n-x)个车站的邮包(n-x)个.
(1)沿途有4个车站(n=4),邮政车在各个车站启程时邮包的总个数为:
在第1个车站(x=1)启程时邮包的总个数:3.
在第2个车站(x=2)启程时邮包的总个数:3-1+2=4.
在第3个车站(x=3)启程时邮包的总个数为:
(2)沿途有n个车站,邮政车在各个车站启程时邮包的总个数为:
在第1个车站(x=1)启程时邮包的总个数:n-1.
在第2个车站(x=2)启程时邮包的总个数:(n-1)-1+(n-2)=2n-4.
依照上述做法,解答下列问题:
①求在第3个车站(x=3)启程时邮包的总个数(应仿照x=2的做法,不能只写最后的结果);
②猜想在第k个车站(x=k)启程时邮包的总个数(用含n,k的代数式表示,可直接写出最后的结果).
(1)沿途有4个车站(n=4),邮政车在各个车站启程时邮包的总个数为:
在第1个车站(x=1)启程时邮包的总个数:3.
在第2个车站(x=2)启程时邮包的总个数:3-1+2=4.
在第3个车站(x=3)启程时邮包的总个数为:
4-2+1=3
.(2)沿途有n个车站,邮政车在各个车站启程时邮包的总个数为:
在第1个车站(x=1)启程时邮包的总个数:n-1.
在第2个车站(x=2)启程时邮包的总个数:(n-1)-1+(n-2)=2n-4.
依照上述做法,解答下列问题:
①求在第3个车站(x=3)启程时邮包的总个数(应仿照x=2的做法,不能只写最后的结果);
②猜想在第k个车站(x=k)启程时邮包的总个数(用含n,k的代数式表示,可直接写出最后的结果).
分析:①随着序号的增加,所有的项也跟着有规律的变化.减去卸下的包裹数,再加上装上的包裹数即可.
②根据理解题意找出题目中所给的等量关系,找出规律,写出邮包个数n的代数式;
②根据理解题意找出题目中所给的等量关系,找出规律,写出邮包个数n的代数式;
解答:解:①在第3个车站(x=3)启程时邮包的总个数为:4-2+1=3.
②由题意得在第k个车站(x=k)启程时邮包的总个数:y=k(n-k).
故答案为:4-2+1=3.
②由题意得在第k个车站(x=k)启程时邮包的总个数:y=k(n-k).
故答案为:4-2+1=3.
点评:本题考查了列代数式,解决此类探究性问题,关键在观察、分析已知数据,寻找它们之间的相互联系,探寻其规律.

练习册系列答案
相关题目
 个车站(包括起点A和终点B),该车在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该车站的邮包一个,还要装上该车站发给后面行程中每个车站的邮包一个.邮车在第1个车站 (A站)启程时要装上该站发给后面行程中每个车站的邮包
个车站(包括起点A和终点B),该车在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该车站的邮包一个,还要装上该车站发给后面行程中每个车站的邮包一个.邮车在第1个车站 (A站)启程时要装上该站发给后面行程中每个车站的邮包 个,邮车上邮包总数是
个,邮车上邮包总数是 个,邮车上邮包总数是 (个).
个,邮车上邮包总数是 (个). 个车站,启程时邮车上邮包总数是多少(用
个车站,启程时邮车上邮包总数是多少(用 ,
, 时,求出邮车上邮包的个数.
时,求出邮车上邮包的个数.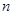 个车站(包括起点A和终点B),该车在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该车站的邮包一个,还要装上该车站发给后面行程中每个车站的邮包一个.邮车在第1个车站 (A站)启程时要装上该站发给后面行程中每个车站的邮包
个车站(包括起点A和终点B),该车在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该车站的邮包一个,还要装上该车站发给后面行程中每个车站的邮包一个.邮车在第1个车站 (A站)启程时要装上该站发给后面行程中每个车站的邮包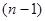 个,邮车上邮包总数是
个,邮车上邮包总数是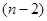 个,邮车上邮包总数是 (个).
个,邮车上邮包总数是 (个).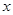 个车站,启程时邮车上邮包总数是多少(用
个车站,启程时邮车上邮包总数是多少(用 ,
,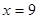 时,求出邮车上邮包的个数.
时,求出邮车上邮包的个数.