题目内容
【题目】在平面直角坐标系中，有一组有规律的点：
A1（0，1）、A2（1，0）、A3（2，1）、A4（3，0）、A5（4，1）….依此规律可知，当n为奇数时，有点An (n－1，1)，当n为偶数时，有点An(n－1，0)．
抛物线C1经过A1，A2，A3三点，抛物线C2经过A2，A3，A4三点，抛物线C3经过A3，A4，A5三点，…抛物线Cn经过An，An＋1，An＋2．
（1）直接写出抛物线C1，C4的解析式；
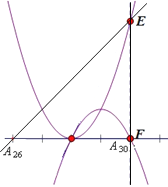
（2）若点E（e，f1）、F（e，f2）分别在抛物线C27、C28上，当e＝29时，求证：△A26EF是等腰直角三角形；
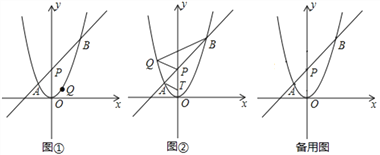
（3）若直线x＝m分别交x轴、抛物线C2014、C2015于点P、M、N，作直线A2015 M、A2015 N，当∠A2015 NM＝90°时，求sin∠A2015 MN的值．
【答案】（1）y1＝(x－1)2， y4＝－(x－4)2＋1；（2）详见解析；（3）
.
【解析】试题分析：(1)根据顶点式即可求出C1，C4的解析式;
(2)由特殊出发,可以发现抛物线C27、C28的解析式应该为: y27＝(x－27)2, y28＝－(x－28)2＋1.则得到点E（29，4）、F（29，0）,根据两点之间的距离公式即可求得EF, 从而说明△A26EF是等腰直角三角形;
(3) 如图，要使∠A2015 NM＝90°，直线x＝m只能在点A2015的右侧，根据三角函数即可得到sin∠A2015 MN的值.
解:（1）根据顶点式容易求出C1，C4的解析式分别为：
y1＝(x－1)2， y4＝－(x－4)2＋1．
（2）由特殊出发，可以发现这组抛物线解析式的特点：
y1＝(x－1)2
y3＝(x－3)2
……
y2＝－(x－2)2＋1
y4＝－(x－4)2＋1
……
∴如图所示，抛物线C27的解析式为：y27＝(x－27)2,且过点A27，A28，A29 ,
抛物线C28的解析式为：y28＝－(x－28)2＋1．且过点A28，A29，A30,
∵点E（e，f1）、F（e，f2）分别在抛物线C27、C28上， e＝29，
∴f1＝(29－27)2＝4，f2＝－(29－28)2+1＝0，
∴点E（e，f1）、F（e，f2）坐标分别为E（29，4）、F（29，0）；
∵A26的坐标是（25，0），点F（29，0）与点A30重合，
∴A26A30＝29－25＝4，EF＝4，且与
轴平行, ∠EF A26=90°,
∴△A26EF是等腰直角三角形；
（3）由（2）中发现的规律可知，
过点
，
过点
，
点A2015坐标为（2014，1）．
如图，要使∠A2015 NM＝90°，直线x＝m只能在点A2015的右侧，
此时，∠A2015 N平行于
轴，
∴PN=1．
∵点N在
上，
∴
， 
或2015（舍去）．
∴∠A2015 N=2，且点M的横坐标为2016．
∴
=－3．
∴MN=1－（－3）=4，A2015 M=
．
，∴sin∠A2015 MN的值为
．
点睛:本题考查了二次函数综合题，涉及的知识点有：顶点式求抛物线的解析式，两点之间的距离公式，勾股定理逆定理，三角函数的知识，综合性较强，有一定的难度.
