Question

（本题10分）如图，矩形OBCD的边OD、OB分别在x轴正半轴和y轴负半轴上，且OD＝10，OB＝8．将矩形的边BC绕点B逆时针旋转，使点C恰好与x轴上的点A重合．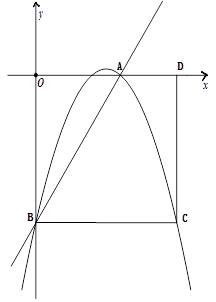

(1)直接写出点A、B的坐标：A(    ，     )、B(     ，     )；
(2)若抛物线y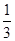＝－x²＋bx＋c经过点A、B，请求出这条抛物线的解析式；
(3)当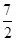≤x≤7，在抛物线上存在点P，使△ABP的面积最大，那么△ABP最大面积是                                 ．（请直接写出结论，不需要写过程）

Answer 1

(1).   A(6,0),B(0,-8)
(2) 
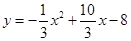
(3) 面积最大为7.

解析试题分析：（1）由OD＝10，OB＝8，矩形的边BC绕点B逆时针旋转，使点C恰好与x轴上的点A重合，可得OA²=AB²－OB²=10²－8²=36，∴OA=6。∴A（6，0），B（0，－8）。
（2）∵抛物线y＝－x²＋b x＋c经过点A、B，
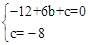∴，解得。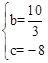
∴这条抛物线的解析式是。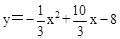
(3)根据二次函数的性质，分≤x＜4，4≤x＜6和6≤x≤7三个区间分别求出最大值，比较即可。
考点：图形的旋转、旋转作图，待定系数法求函数解析式
点评：弄懂旋转的性质：旋转点到中心的距离相等，对应点与旋转中心所连线段的夹角等于旋转角，旋转前后的图形全等。