题目内容
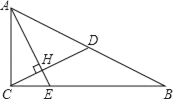
【题目】如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D,E分别在边AB,AC上,将△ADE沿直线DE翻折,点A的对应点在边AB上,联结A′C,如果A′C=A′A,那么BD=___.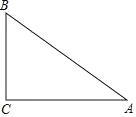
【答案】![]()
【解析】
根据勾股定理得到AB=10,根据等腰三角形的性质得到∠A=∠ACA,根据余角的性质得到∠B=∠BCA,得到AA=AB=![]() AB=5,根据折叠的性质得到AD=AD=
AB=5,根据折叠的性质得到AD=AD=![]() ,于是得到结论
,于是得到结论
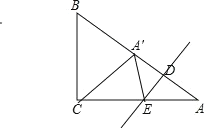
∵在Rt△ABC中,∠C=90°,AC=8,BC=6,
∴AB=10,
∵A′C=A′A,
∴∠A=∠A′CA,
∵∠ACB=90°,
∴∠B+∠A=∠BCA′+∠A′CA=90°,
∴∠B=∠BCA′,
∴AA′=A′B=![]() AB=5,
AB=5,
∵将△ADE沿直线DE翻折,
∴A′D=AD=![]() ,
,
∴BD=A′B+A′D=![]() ,
,
故答案为:![]()

练习册系列答案
相关题目