题目内容
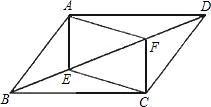
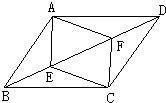 20、如图,E、F是平行四边形ABCD对角线上的两点,给出下列三个条件:①BE=DF;②AF=CE;③∠AEB=∠CFD.
20、如图,E、F是平行四边形ABCD对角线上的两点,给出下列三个条件:①BE=DF;②AF=CE;③∠AEB=∠CFD.(1)在上述三个条件中,能够使四边形AECF是平行四边形的条件有
①③
(只需填写序号);(2)从(1)中选择一个加以证明.
分析:根据(1)的已知条件,利用平行四边形ABCD,证得AE=FC,AF=EC即可证明四边形AECF是平行四边形.
解答:解:(1)①③;
(2)证明:
∵平行四边形ABCD,
∴AB=CD,∠ADF=∠EBC.
又∵BE=DF,
∴△BEA≌△DFC.
∴AE=FC.
同理可证:△DFA≌△BEC从而得AF=EC.
∴四边形AECF是平行四边形.
(2)证明:
∵平行四边形ABCD,
∴AB=CD,∠ADF=∠EBC.
又∵BE=DF,
∴△BEA≌△DFC.
∴AE=FC.
同理可证:△DFA≌△BEC从而得AF=EC.
∴四边形AECF是平行四边形.
点评:本题考查了平行四边形的判定与性质,熟练掌握性质定理和判定定理是解题的关键.平行四边形的五种判定方法与平行四边形的性质相呼应,每种方法都对应着一种性质,在应用时应注意它们的区别与联系.

练习册系列答案
相关题目
 8、
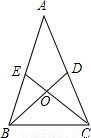
8、 1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
 相交于点C.
相交于点C.
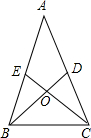 1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.