��Ŀ����
����Ŀ�����Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ�
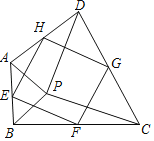
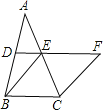
��1����ͼ����P���ı���ABCD��һ�㣬������PA��PB��PC��PD����APB����CPD����E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣬�����е��ı���EFGH����״����֤����IJ��룻
��2�����ı䣨1���е�������ʹ��APB����CPD��90���������������䣬ֱ��д���е��ı���EFGH����״������֤������
���𰸡���1���ı���EFGH�����Σ����ɼ���������2���ı���EFGH�������Σ����ɼ�����
��������
��1������AC��BD����PA��PB��PC��PD����APB����CPD��֤��APC�ա�BPD��SAS����
�ʿɵõ�AC��BD�������������ε���λ�߿ɵ�EF��![]() AC��FG��
AC��FG��![]() BD��EH��
BD��EH��![]() BD��GH��
BD��GH��![]() AC����֤EF��FG��GH��EH�����ı���EFGH�����Σ�
AC����֤EF��FG��GH��EH�����ı���EFGH�����Σ�
��2����AC��BD����ΪO��AC��PD���ڵ�M��AC��EH���ڵ�N��
���á�APC�ա�BPD�����ԡ�ACP����BDP���ٸ��ݡ�CPD��90���ʡ�PDC+��PCD��90��
�á�ODC+��OCD��90��������COD��90������AC��BD����������λ�ߵ����ʡ�EHG����ENO����BOC����DOC��90�������ɵõ��ı���EFGH�������Σ�
��1���ı���EFGH�����Σ�
��ͼ������AC��BD��
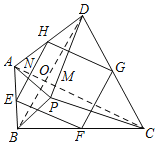
�ߡ�APB����CPD��
���APB+��APD����CPD+��APD������APC����BPD��
�ڡ�APC�͡�BPD�У�
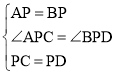 ��
��
���APC�ա�BPD��SAS����
��AC��BD��
�ߵ�E��F��G�ֱ�ΪAB��BC��CD���е㣬
��EF��![]() AC��FG��
AC��FG��![]() BD��EH��
BD��EH��![]() BD��GH��
BD��GH��![]() AC��
AC��
��EF��FG��GH��EH��
���ı���EFGH�����Σ�
��2���ı���EFGH�������Σ�
��AC��BD����ΪO��AC��PD���ڵ�M��AC��EH���ڵ�N��
�ߡ�APC�ա�BPD��
���ACP����BDP��
�ߡ�CPD��90��
���PDC+��PCD��90��
���ODC+��OCD��90��
���COD��90��
��AC��BD
��EH��BD��AC��HG��
���EHG����ENO����BOC����DOC��90����
���ı���EFGH�����Σ�
���ı���EFGH�������Σ�

 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�