题目内容
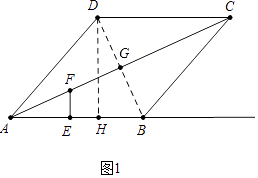
【题目】如图1,在边长为5的菱形ABCD中,cos∠BAD= ![]() ,点E是射线AB上的点,作EF⊥AB,交AC于点F.
,点E是射线AB上的点,作EF⊥AB,交AC于点F. 
(1)求菱形ABCD的面积;
(2)求证:AE=2EF;
(3)如图2,过点F,E,B作⊙O,连结DF,若⊙O与△CDF的边所在直线相切,求所有满足条件的AE的长度. 
【答案】
(1)解:如图1中,作DH⊥AB于H.
在Rt△ADH中,∵∠AHD=90°,AD=5,cos∠DAH= ![]() ,
,
∴AH=3,DH= ![]() =4,
=4,
∴S菱形ABCD=ABDH=5×4=20.
(2)解:证明:如图1中,BD与AC交于点G.
在Rt△DHB中,∵DH=4,BH=2,
∴BD= ![]() =
= ![]() =2
=2 ![]() ,
,
∵四边形ABCD是菱形,
∴AC⊥BD,BG=DG= ![]() ,AG=
,AG= ![]() =
= ![]() =2
=2 ![]() ,
,
∵∠EAF=∠BAG,∠AEF=∠AGB=90°,
∴△AEF∽△AGB,
∴ ![]() =
= ![]() =
= ![]() =2,
=2,
∴AE=2EF.
(3)解:①如图2中,当⊙O与直线DF相切时,易知,∠BFD=90°,DF=BF.
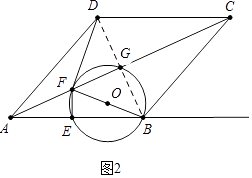
∵BD=2 ![]() ,
,
∴BF= ![]() ,设EF=x,则AE=2EF=2x,
,设EF=x,则AE=2EF=2x,
在Rt△BEF中,∵BF2=EF2+BE2,
∴10=x2+(5﹣2x)2,
解得x=1或3,
∴AE=2或6时,⊙O与直线DF相切.
②如图3中,当⊙O与AC相切时,易知点F与G重合,设EF=x,AE=2x,
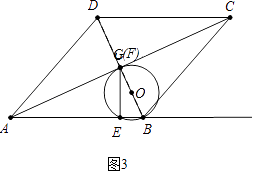
在Rt△AFE中,∵AG2=AE2+GE2,
∴20=4x2+x2,
∴x2=4,
∴x=2,
∴AE=4时,⊙O与直线CF相切.
③如图4中,当⊙O与CD相切于点M,延长MO交AE与H,设EF=x,则AE=2x,则OH= ![]() EF=
EF= ![]() x,BF=
x,BF= ![]() ,
,
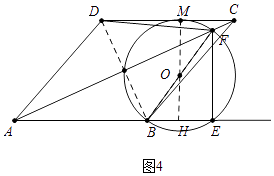
∵HM=4,
∴OM+OH=4,
∴ ![]() +
+ ![]() x=4,
x=4,
整理得,4x2﹣4x﹣39=0,
解得x= ![]() 或
或 ![]() (舍弃),
(舍弃),
∴AE=1+2 ![]() ,
,
综上所述,满足条件的AE的值为2或4或6或1+2 ![]() .
.
【解析】(1)如图1中,作DH⊥AB于H.在Rt△ADH中,由∠AHD=90°,AD=5,cos∠DAH= ![]() ,推出AH=3,DH=
,推出AH=3,DH= ![]() =4,即可解决问题;(2)如图1中,BD与AC交于点G.在Rt△DHB中,可得BD=
=4,即可解决问题;(2)如图1中,BD与AC交于点G.在Rt△DHB中,可得BD= ![]() =
= ![]() =2
=2 ![]() ,由四边形ABCD是菱形,推出AC⊥BD,BG=DG=
,由四边形ABCD是菱形,推出AC⊥BD,BG=DG= ![]() ,AG=
,AG= ![]() =
= ![]() =2
=2 ![]() ,由△AEF∽△AGB,推出
,由△AEF∽△AGB,推出 ![]() =
= ![]() =
= ![]() =2,即可解决问题;(3)分三种情形分别求解:①如图2中,当⊙O与直线DF相切时.②如图3中,当⊙O与AC相切时.③如图4中,当⊙O与CD相切于点M.分别求解即可;
=2,即可解决问题;(3)分三种情形分别求解:①如图2中,当⊙O与直线DF相切时.②如图3中,当⊙O与AC相切时.③如图4中,当⊙O与CD相切于点M.分别求解即可;