Question

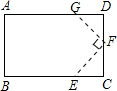如图，一张长方形纸片剪去两个角，测得EF⊥GF，∠AGF=135°，则∠BEF=

1. A.
   135°
2. B.
   140°
3. C.
   145°
4. D.
   150°

Answer 1

A
分析：过F作FM∥AD，交AB于M，根据矩形性质得出AD∥BC∥FM，推出∠AGF+∠GFM=180°，∠MFE+∠BEF=180°，把∠AGF=135°，∠GFE=90°代入求出即可．
解答：
过F作FM∥AD，交AB于M，
∵四边形ABCD是矩形，
∴AD∥BC，
∴AD∥FM∥BC，
∴∠AGF+∠GFM=180°，
∵∠AGF=135°，
∴∠GFM=45°，
∵EF⊥FG，
∴∠GFE=90°，
∴∠MFE=90°-45°=45°，
∵FM∥BC，
∴∠BEF=180°-45°=135°，
故选A．
点评：本题考查了矩形性质和平行线的性质，主要考查学生的推理能力和计算能力．