题目内容
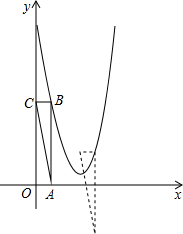（2010•邢台一模）在平面直角坐标系中，抛物线y=ax2-6x+c经过点（0，10）和点（3，1）．（1）求这条抛物线的函数表达式，并求出它的对称轴；
（2）如图，△ABC的顶点B在抛物线y=ax2-6x+c上，顶点C在y轴上，顶点A在x轴上，且BC=1，∠ABC=90°，求AC的长；
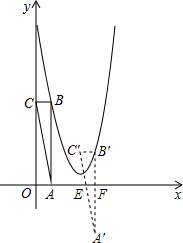
（3）△ABC的顶点B沿抛物线y=ax2-6x+c移动，移动过程中，边BC与x轴保持平行，当△ABC被x轴分成上下两部分的面积比为3：1时，求点C的坐标．
分析：（1）将点（0，10）和点（3，1）代入解析式就可以求出抛物线的解析式，然后将解析式化为顶点式就可以求出对称轴．
（2）由BC=1，∠ABC=90°，就可以求得B点的横坐标，将点B的横坐标代入解析式就可以求出B点的纵坐标从而求出AB的值，再由勾股定理就可以求出AC的值．
（3）如图，当△ABC移到△A′B′C′的位置时，S四边形EFB′C′：S△EFA′=3：1，有S△A′B′C′：S△EFA′=4：1，由相似三角形的性质可以求出B′F，求得B′的纵坐标，代入抛物线的解析式就可以求出B′的横坐标，从而求得C′的坐标．
（2）由BC=1，∠ABC=90°，就可以求得B点的横坐标，将点B的横坐标代入解析式就可以求出B点的纵坐标从而求出AB的值，再由勾股定理就可以求出AC的值．
（3）如图，当△ABC移到△A′B′C′的位置时，S四边形EFB′C′：S△EFA′=3：1，有S△A′B′C′：S△EFA′=4：1，由相似三角形的性质可以求出B′F，求得B′的纵坐标，代入抛物线的解析式就可以求出B′的横坐标，从而求得C′的坐标．
解答：解：（1）由题意，得
，
解得：
，
∴抛物线的解析式为：y=x2-6x+10
∴y=（x-3）2+1
∴抛物线的对称轴是：x=3．
（2）∵BC=1，∠ABC=90°，
∴B点的横坐标为1，
∴y=1-6+10=5，
∴AB=5，在Rt△ABC中，由勾股定理，得AC=
；
（3）∵△A′B′C′是由△ABC平移得到的，
∴△A′B′C′≌△ABC，
∴A′B′=AB=5．
∵S四边形EFB′C′：S△EFA′=3：1，
∴S△A′B′C′：S△EFA′=4：1，
∵BC与x轴保持平行，
∴△A′B′C∽△EFA
∴
=2，
∴A′F=
，
∴B′F=
，
∴
=x2-6x+10，
∴x1=
，x2=
，
故C（
，
）或（
，
）．
|
解得：
|
∴抛物线的解析式为：y=x2-6x+10
∴y=（x-3）2+1
∴抛物线的对称轴是：x=3．
（2）∵BC=1，∠ABC=90°，
∴B点的横坐标为1，
∴y=1-6+10=5，
∴AB=5，在Rt△ABC中，由勾股定理，得AC=
| 26 |
（3）∵△A′B′C′是由△ABC平移得到的，
∴△A′B′C′≌△ABC，
∴A′B′=AB=5．
∵S四边形EFB′C′：S△EFA′=3：1，
∴S△A′B′C′：S△EFA′=4：1，
∵BC与x轴保持平行，
∴△A′B′C∽△EFA
∴
| A′B′ |
| A′F |
∴A′F=
| 5 |
| 2 |
∴B′F=
| 5 |
| 2 |
∴
| 5 |
| 2 |
∴x1=
6+
| ||
| 2 |
6-
| ||
| 2 |
故C（
4+
| ||
| 2 |
| 5 |
| 2 |
4-
| ||
| 2 |
| 5 |
| 2 |
点评：本题是一道二次函数的综合试题，考查了待定系数法求函数的解析式，勾股定理的运用，二次函数图象与几何变换，平移的性质及运用，相似三角形的性质．
练习册系列答案
相关题目
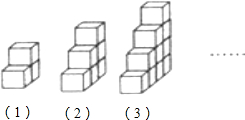第n（n≥1）个几何体中，小正方体的个数为（ ）