题目内容
(2010•邢台一模)在图中,各几何体都是由大小相同的小正方体按一定规律垒成的,那么,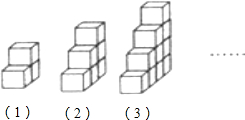 第n(n≥1)个几何体中,小正方体的个数为( )
第n(n≥1)个几何体中,小正方体的个数为( )
 第n(n≥1)个几何体中,小正方体的个数为( )
第n(n≥1)个几何体中,小正方体的个数为( )分析:观察图形可知,第一个几何体小正方形有
=3个,第二个几何体小正方形有
=6个,第三个几何体小正方形有
=10个,继而即可求出第n个几何体中小正方形的个数.
| (1+1)(1+2) |
| 2 |
| (2+1)(2+2) |
| 2 |
| (3+1)(3+2) |
| 2 |
解答:解:由题意得:第一个几何体中,小正方形的个数为
=3个,
第二个几何体中,小正方形的个数为
=6个,
第三个几何体中,小正方形的个数为
=10个,
…,
∴第n个几何体中小正方形的个数为
.
故选C.
| (1+1)(1+2) |
| 2 |
第二个几何体中,小正方形的个数为
| (2+1)(2+2) |
| 2 |
第三个几何体中,小正方形的个数为
| (3+1)(3+2) |
| 2 |
…,
∴第n个几何体中小正方形的个数为
| (n+1)(n+2) |
| 2 |
故选C.
点评:此题考查的知识点是图形数字的变化类问题,关键是由已知观察分析总结出规律,按规律求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
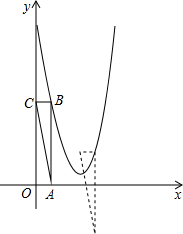 (2010•邢台一模)在平面直角坐标系中,抛物线y=ax2-6x+c经过点(0,10)和点(3,1).
(2010•邢台一模)在平面直角坐标系中,抛物线y=ax2-6x+c经过点(0,10)和点(3,1).