Question

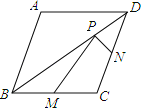
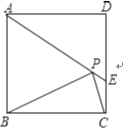
【题目】如图，在正方形ABCD中，AD=，把边BC绕点B逆时针旋转30°得到线段BP，连接AP并延长交CD于点E，连接PC，则三角形PCE的面积为____________．

Answer 1

【答案】

【解析】分析：根据旋转的想知道的PB=BC=AB，∠PBC=30°，推出△ABP是等边三角形，得到∠BAP=60°，AP=AB=2，解直角三角形得到CE=2-2，PE=4-2，过P作PF⊥CD于F，即可解答．

详解：如图：过P作PF⊥CD于F.

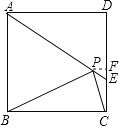
∵四边形ABCD是正方形，

∴∠ABC=90°，

∵把边BC绕点B逆时针旋转30°得到线段BP，

∴PB=BC=AB,∠PBC=30°，

∴∠ABP=60°，

∴△ABP是等边三角形，

∴∠BAP=60°,AP=AB=2，

∵AD=2，

∴AE=4，DE=2，

∴CE=22,PE=42，

∴PF=PE=23，

∴三角形PCE的面积=CEPF=×(22)×(23)=95，

故答案为：95.