题目内容
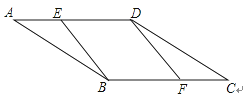
【题目】如图，在平行四边形ABCD中，AE⊥BC于E，AF⊥CD于F，∠EAF=45°，且AE+AF=2
， 则平行四边形ABCD的周长是（ ）
A.2
B.4?
C.4
D.8
【答案】D
【解析】解：∵AE⊥BC，AF⊥CD，∠EAF=45°，
∴∠C=180°﹣90°﹣90°﹣45°=135°，
∵四边形ABCD是平行四边形，
∴∠B=∠D=180°﹣∠C=45°，
∴AB=
AE，AD=AF，
∴AB+AD=（AE+AF）=×2=4，
∴平行四边形ABCD的周长是：4×2=8．
故选D．
由AE⊥BC于E，AF⊥CD于F，∠EAF=45°，易求得∠C的度数，又由在平行四边形ABCD中，证得△ABE与△ADF是等腰直角三角形，继而求得答案．
练习册系列答案
中考解读考点精练系列答案
相关题目
