题目内容
两相似等腰三角形的斜边长分别为2和8，则他们的面积之比为
- A.1：2
- B.1：4
- C.1：16
- D.1：8
C
分析：两相似等腰三角形的斜边长分别为2和8，它们的相似比为1：4，再根据相似三角形的面积比等于相似比的平方，即可求．
解答：根据题意，
∵相似比=2：8=1：4
∴面积比=1：16．
故选C．
点评：此题要先利用相似三角形的性质，然后再利用面积比等于相似比的平方就可计算．
分析：两相似等腰三角形的斜边长分别为2和8，它们的相似比为1：4，再根据相似三角形的面积比等于相似比的平方，即可求．
解答：根据题意，
∵相似比=2：8=1：4
∴面积比=1：16．
故选C．
点评：此题要先利用相似三角形的性质，然后再利用面积比等于相似比的平方就可计算．
练习册系列答案
相关题目
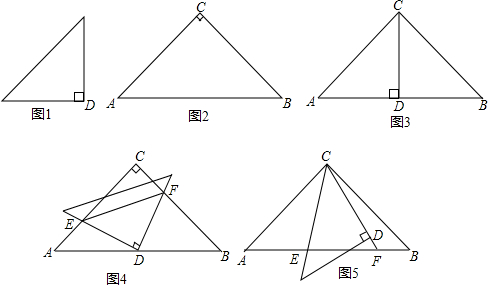
的等腰直角三角形，将两个三角形如图3放置，小直角三角形的斜边与大直角三角形的一直角边重合．
的等腰直角三角形，将两个三角形如图3放置，小直角三角形的斜边与大直角三角形的一直角边重合．
的等腰直角三角形，将两个三角形如图3放置，小直角三角形的斜边与大直角三角形的一直角边重合．