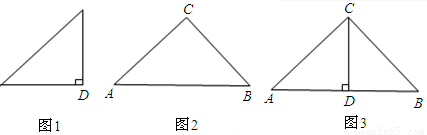
题目内容
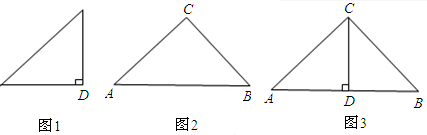
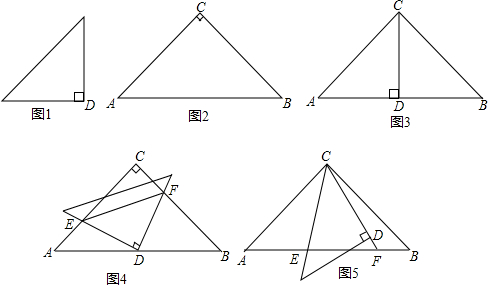
图1、2是两个相似比为1: 的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.
的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.(1)图3中,绕点D旋转小直角三角形,使两直角边分别与AC、BC交于点E、F,如图4,①求证:DE=DF.②求证:AE2+BF2=EF2;
(2)在图3中,绕点C旋转小直角三角形,使它的斜和CD延长线分别与交于点,如图5,证明结论:AE2+BF2=EF2仍成立.

【答案】分析:(1)①连接CD,得出AD=CD,求出∠1=∠3,证出△CDF≌△ADE即可;②由△CDF≌△ADE得出AE=CF,同理证△CED≌△BFD,推出BF=CE,在△CEF中根据勾股定理得出CE2+CF2=EF2,代入求出即可;
(2)把△CFB绕点C顺时针旋转90°得到△CGA,连接GE,求出∠GCE=∠ECF,CG=CF,根据SAS证△CGE≌△CFE,推出GE=EF,根据勾股定理求出即可.
解答:(1)①证明:如右图4,连接CD,
∵图1、2是两个相似比为1: 的等腰直角三角形,
的等腰直角三角形,
∴放置后小直角三角形的斜边正好是大直角三角形的直角边,
∴D为AB中点,CD⊥AB,
∵∠ACB=90°,
∴CD=AD=BD,
∴∠4=∠A=45°,
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
在△CDF和△ADE中
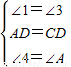 ,
,
∴△CDF≌△ADE,
∴DE=DF.
②证明:∵由①知△CDF≌△ADE,
∴CF=AE,
与①证明△CDF≌△ADE类似可证△CED≌△BFD,
得出CE=BF,
∵在△CEF中,CE2+CF2=EF2,
∴AE2+BF2=EF2.
(2)证明:把△CFB绕点C顺时针旋转90°得到△CGA,如右图5,连接GE,
∵根据旋转得出:CF=CG,AG=BF,∠4=∠1,∠B=∠GAC=45°,
∴∠GAE=90°,
∵∠3=45°,
∴∠2+∠4=90°-45°=45°,
∴∠1+∠2=45°,
∵在△CGE和△CFE中
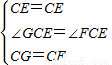 ,
,
∴△CGE≌△CFE,
∴GE=EF,
∵在Rt△AGE中,AE2+AG2=GE2,
∴AE2+BF2=EF2.
点评:本题考查了等腰直角三角形,勾股定理,全等三角形的性质和判定,旋转的性质的应用,通过做此题培养了学生的分析问题和解决问题的能力,题目具有一定的代表性,是一道比较好的题目,注意:此类问题证明过程类似.
(2)把△CFB绕点C顺时针旋转90°得到△CGA,连接GE,求出∠GCE=∠ECF,CG=CF,根据SAS证△CGE≌△CFE,推出GE=EF,根据勾股定理求出即可.
解答:(1)①证明:如右图4,连接CD,

∵图1、2是两个相似比为1:
 的等腰直角三角形,
的等腰直角三角形,∴放置后小直角三角形的斜边正好是大直角三角形的直角边,
∴D为AB中点,CD⊥AB,
∵∠ACB=90°,
∴CD=AD=BD,
∴∠4=∠A=45°,
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
在△CDF和△ADE中
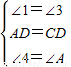 ,
,∴△CDF≌△ADE,
∴DE=DF.
②证明:∵由①知△CDF≌△ADE,
∴CF=AE,
与①证明△CDF≌△ADE类似可证△CED≌△BFD,
得出CE=BF,
∵在△CEF中,CE2+CF2=EF2,
∴AE2+BF2=EF2.
(2)证明:把△CFB绕点C顺时针旋转90°得到△CGA,如右图5,连接GE,

∵根据旋转得出:CF=CG,AG=BF,∠4=∠1,∠B=∠GAC=45°,
∴∠GAE=90°,
∵∠3=45°,
∴∠2+∠4=90°-45°=45°,
∴∠1+∠2=45°,
∵在△CGE和△CFE中
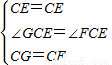 ,
,∴△CGE≌△CFE,
∴GE=EF,
∵在Rt△AGE中,AE2+AG2=GE2,
∴AE2+BF2=EF2.
点评:本题考查了等腰直角三角形,勾股定理,全等三角形的性质和判定,旋转的性质的应用,通过做此题培养了学生的分析问题和解决问题的能力,题目具有一定的代表性,是一道比较好的题目,注意:此类问题证明过程类似.

练习册系列答案
相关题目
 的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.
的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.
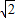 的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.
的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.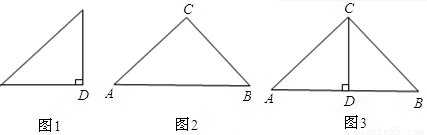

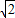 的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.
的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.