题目内容
（2012•盐城二模）如图，将半径为2的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长为2
| 3 |
2
．| 3 |
分析：作OD⊥AB于D，连接OA，先根据勾股定理得AD的长，再根据垂径定理得AB的长．
解答：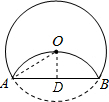
解：作OD⊥AB于D，连接OA．
∵OD⊥AB，OA=2，
∴OD=
OA=1，
在Rt△OAD中
AD=
=
=
，
∴AB=2AD=2
．
故答案为：2
．
解：作OD⊥AB于D，连接OA．∵OD⊥AB，OA=2，
∴OD=
| 1 |
| 2 |
在Rt△OAD中
AD=
| OA2-OD2 |
| 22-12 |
| 3 |
∴AB=2AD=2
| 3 |
故答案为：2
| 3 |
点评：本题考查的是垂径定理的应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
