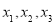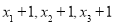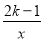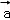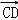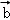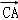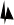题目内容
已知梯形ABCD中,AD∥BC,AD=1,BC=2,sinB=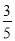 ,过点C在∠BCD的内部作射线交射线BA于点E,使得∠DCE=∠B.
,过点C在∠BCD的内部作射线交射线BA于点E,使得∠DCE=∠B.

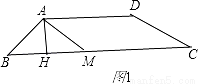
(1)如图1,当ABCD为等腰梯形时,求AB的长;
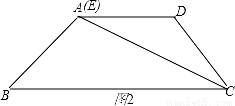
(2)当点E与点A重合时(如图2),求AB的长;
(3)当△BCE为直角三角形时,求AB的长.
(1)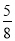 ;(2)
;(2)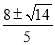 ;(3)
;(3)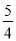 或
或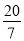 .
.
【解析】
试题分析:(1)作AM∥DC交BC于点M,AH⊥BC于点H,AD=1,BC=2,sinB=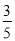 ,得到AM=AB,BH=HM=
,得到AM=AB,BH=HM=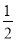 ,结合三角函数的定义可以求得AB的长.
,结合三角函数的定义可以求得AB的长.
(2))由AD∥BC得到∠DAC=∠ACB,又∵∠DCE=∠B,∴△ADC∽△CAB,得到AC2=AD•BC,求得AC的长度,结合勾股定理,即可构造出关于AB的方程,解方程即可求得相应的AB的长度.
(3)分两种情况来讨论:如图3-1,当BE⊥CE时,∵∠DCE=∠B,∠B+∠BCE=90°,∴∠DCE+∠BCE=90°,作AH⊥BC,则HC=AD=1,∴BH=BC-HC=2-1=1,由sinB即可求得cosB的值,继而求得AB的长度;如图3-2,当BC⊥CE时,延长DA交CE的延长线于点F,由△FDC∽△CEB,可以得到AE的长度,继而求得AB的长度.
试题解析:(1)如图1,作AM∥DC交BC于点M,作AH⊥BC于点H,
∵AD∥BC,∴AMCD为平行四边形,
∴AM=DC,MC=AD=1,
∴BM=BC-MC=2-1=1,
∵四边形ABCD为等腰梯形,
∴AB=DC,∴AB=AM,∴BH=HM=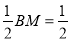
在直角三角形ABH中,
∵sinB=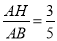 ,
,
∴cosB=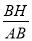 ,∵
,∵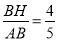 ,∴
,∴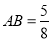 .
.
(2)如图2,∵AD∥BC,
∴∠DAC=∠ACB,
又∵∠DCE=∠B,
∴△ADC∽△CAB,
∴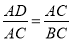 ,
,
∴AC2=AD•BC=2,
作AF⊥BC于点F,
设AB=x,∵sinB=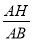 ,
,
∴AF=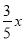 ,BF=
,BF=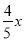 ,
,
∴CF=2-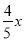 ,
,
在直角三角形AFC中,AF2+CF2=AC2,即: ,
,
∴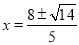 ,
,
即当点A与点E重合时,AB=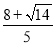 ,或者AB=
,或者AB=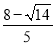 .
.
(3)∵△BCE为直角三角形,
∴BE⊥CE或BC⊥CE,
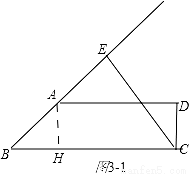
情况一,当BE⊥CE时,如图3-1,
∵∠DCE=∠B,∠B+∠BCE=90°,
∴∠DCE+∠BCE=90°,
作AH⊥BC,则HC=AD=1,
∴BH=BC-HC=2-1=1,
又由sinB=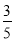 可得,cosB=
可得,cosB=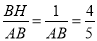 ,
,
解得:AB=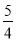 .
.
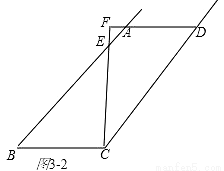
情况二,当BC⊥CE时,如图3-2,
延长DA交CE的延长线于点F,设AE=a,则AF=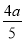 ,EF=
,EF=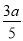 ,
,
在直角三角形BCE中,
∵BC=2,sinB=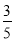 ,
,
∴BE=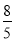 ,EC=
,EC=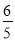 ,
,
∵AD∥BC,BC⊥CE,
∴AD⊥EC,
又∵∠DCE=∠B,
∴△FDC∽△CEB,
∴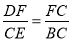 ,即DC·BC=FC·CE,
,即DC·BC=FC·CE,
∴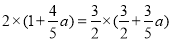 ,
,
∴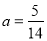 .
.
∴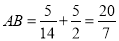
∴当△BCE为直角三角形时,AB=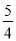 或AB=
或AB=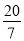 .
.
考点:相似形综合题.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案汶川地震牵动着全国亿万人民的心,某校为地震灾区开展了“献出我们的爱”赈灾捐款活动.八年级(1)班50名同学积极参加了这次赈灾捐款活动,下表是小明对全班捐款情况的统计表:
捐款(元) | 10 | 15 | 30 |
| 50 | 60 |
人数 | 3 | 6 | 11 |
| 13 | 6 |
因不慎两处被墨水污染,已无法看清,但已知全班平均每人捐款38元.
(1)根据以上信息请帮助小明计算出被污染处的数据,并写出解答过程.
(2)该班捐款金额的众数,中位数分别是多少?