题目内容
 如图,已知△ABC为等边三角形,M为三角形外任意一点.
如图,已知△ABC为等边三角形,M为三角形外任意一点.
(1)请你借助旋转知识说明AM≤BM+CM;
(2)线段AM是否存在最大值?若存在,请指出存在的条件;若不存在,请说明理由.
解:(1)将△BMC绕B点逆时针方向旋转,使C点与A点重合,得△BM′A,
∵∠MBM′=60°,BM=BM′,AM′=MC.
∴△BMM′为正三角形.
∴MM′=BM.
①若M′在AM上,
则AM=AM′+MM′=BM+MC,
②若M′不在AM上,连接AM′、MM′,
在△AMM′中,根据三角形三边关系可知:
AM<AM′+MM′,
∴AM<BM+MC,
综上所述:AM≤BM+CM;
(2)线段AM有最大值.
当且仅当M′在AM上时,AM=BM+MC;
存在的条件是:∠BMC=120°.
分析:(1)应把AM和BM所在的三角形旋转,与AM组成三角形,将△BMC绕B点逆时针方向旋转,使C点与A点重合,得△BM′A,易得△BMM′为正三角形,根据三角形三边关系即可证明.
(2)由(1)得线段AM存在最大值,M′在AM上时.
点评:求三边关系,那么这三边应在一个三角形中,可通过旋转得到.
∵∠MBM′=60°,BM=BM′,AM′=MC.
∴△BMM′为正三角形.
∴MM′=BM.
①若M′在AM上,
则AM=AM′+MM′=BM+MC,
②若M′不在AM上,连接AM′、MM′,
在△AMM′中,根据三角形三边关系可知:
AM<AM′+MM′,
∴AM<BM+MC,
综上所述:AM≤BM+CM;
(2)线段AM有最大值.
当且仅当M′在AM上时,AM=BM+MC;
存在的条件是:∠BMC=120°.
分析:(1)应把AM和BM所在的三角形旋转,与AM组成三角形,将△BMC绕B点逆时针方向旋转,使C点与A点重合,得△BM′A,易得△BMM′为正三角形,根据三角形三边关系即可证明.
(2)由(1)得线段AM存在最大值,M′在AM上时.
点评:求三边关系,那么这三边应在一个三角形中,可通过旋转得到.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
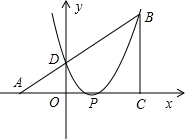 ,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的二次函数图象经过点B、D.
,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的二次函数图象经过点B、D. 如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D.
如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D. 25、如图,已知△ABC为等边三角形,D、F分别为BC、AB边上的点,CD=BF,以AD为边作等边△ADE.
25、如图,已知△ABC为等边三角形,D、F分别为BC、AB边上的点,CD=BF,以AD为边作等边△ADE. 如图,已知△ABC为等边三角形,D,E,F分别在边BC,CA,AB上,且△DEF也是等边三角形,除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的.
如图,已知△ABC为等边三角形,D,E,F分别在边BC,CA,AB上,且△DEF也是等边三角形,除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的. 如图,已知△ABC为等边三角形,点D.E分别在BC.AC边上,且AE=CD,AD与BE相交于点F.
如图,已知△ABC为等边三角形,点D.E分别在BC.AC边上,且AE=CD,AD与BE相交于点F.