题目内容
【题目】如图，直线y=﹣3x+3与x轴、y轴分别交于点A、B，抛物线y=a（x﹣2）2+k经过点A、B．求：
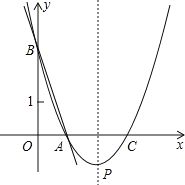
（1）点A、B的坐标；
（2）抛物线的函数表达式；
（3）在抛物线对称轴上是否存在点P，使得以A、B、P为顶点的三角形为等腰三角形？若存在，求点P的坐标；若不存在，请说明理由．
【答案】（1）A（1，0）、B（0，3）．（2）y=（x﹣2）2﹣1．（3）所求的点为P1（2，3），P2（2，3+
），P3（2，3﹣），P4（2，2）．
【解析】
试题分析：（1）由y=﹣3x+3得，当x=0时，y=3；当y=0时，x=1，即可确定点A，B的坐标；
（2）把点A（1，0）、B（0，3）代入y=a（x﹣2）2+k得：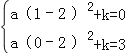
，解得
，即可解答；
（3）存在，由AO=1，BO=3，得到AB=
．设对称x轴交于点D，P（2y），D（2，0），所以DA=1，PD=|y|，PA2=PD2+DA2=y2+1，分三种情况讨论解答：当PA=AB即PA2=AB2=10时；当PB=AB即PB2=AB2=10时；当PA=PB即PA2=PB2时．
解：（1）由y=﹣3x+3得，当x=0时，y=3；当y=0时，x=1
∴A（1，0）、B（0，3）．
（2）把点A（1，0）、B（0，3）代入y=a（x﹣2）2+k得：
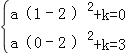
解得
∴抛物线的函数表达式为y=（x﹣2）2﹣1．
（3）∵AO=1，BO=3，
∴AB=
．
设对称x轴交于点D，P（2，y），D（2，0），
∴DA=1，PD=|y|，PA2=PD2+DA2=y2+1，
当PA=AB即PA2=AB2=10时，
∴y2+1=10，
解得y=±3
∴P（2，±3），
但当P（2，﹣3）时，P、A、B在同一条直线上，不合题意舍去．
∴P1（2，3），
当PB=AB即PB2=AB2=10时，如图，过B作BE⊥对称轴于点E，
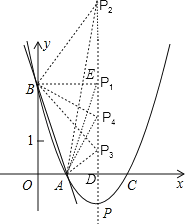
则E（2，3），EB=2，PE2=（y﹣3）2，
∴PB2=PE2+BE2=（y﹣3）2+4=10，
解得
∴P2（2，3+）、P3（2，3﹣），当PA=PB即PA2=PB2时，
y2+1=（y﹣3）2+4
解得y=2，
∴P4（2，2）．
综上所述，所求的点为P1（2，3），P2（2，3+），P3（2，3﹣），P4（2，2）．
